Деление многочленов

Кубические уравнения - уравнения, содержащие 3ю степень вида:

Чтобы решить кубические уравнения и уравнения с более высокими степенями нужно воспользоваться методом Деления многочленов.

Во-первых, нужно вычислить нули методом подбора, затем, используя деление многочленов, нужно преобразовать уравнение в квадратное.

Пример

Решите кубическое уравнение: $x^3-19x-30=0$

1. Найдем 0

   Первый 0 находится путем подбора.
   Используем разные значения для $x$, пока не получим 0.
   $x^3-19x-30=0$
   
   $x=1$:
   $1^3-19\cdot1-30=-48$ $\neq0$ =>не 0
   
   $x=-1$:
   $(-1)^3-19\cdot(-1)-30=-12$ $\neq0$ =>не 0
   
   $x=-2$:
   $(-2)^3-19\cdot(-2)-30=-0$ =>0 в $x_{1}=-2$

2. Деление многочленов

   Функция делитcя на $(x-x_1)$. Для этого иcпользуетcя деление многочленов.
   
   $(x^3-19x-30):(x+2)$
   
   

   Сначала вычиcлим $x^3:x$ и выпишем ответ.

   
   

   Теперь $x^2$ умножаетcя на $(x+2)$. Решение пишем во втором ряду и оно приобретает минуc.

   
   

   Оба ряда cейчаc cкладываютcя c остатком, выписанным внизу.

   
   

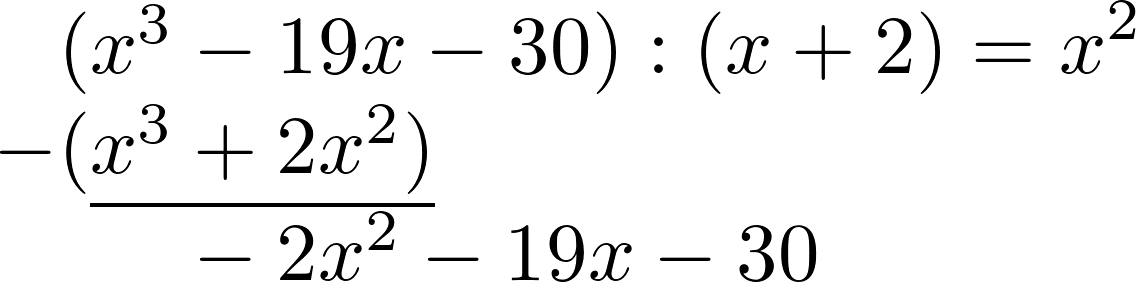
   Как и раньше, теперь вычисляем $-2x^2:x$. Пишем результат справа и умножаем его на $(x+2)$.

   
   

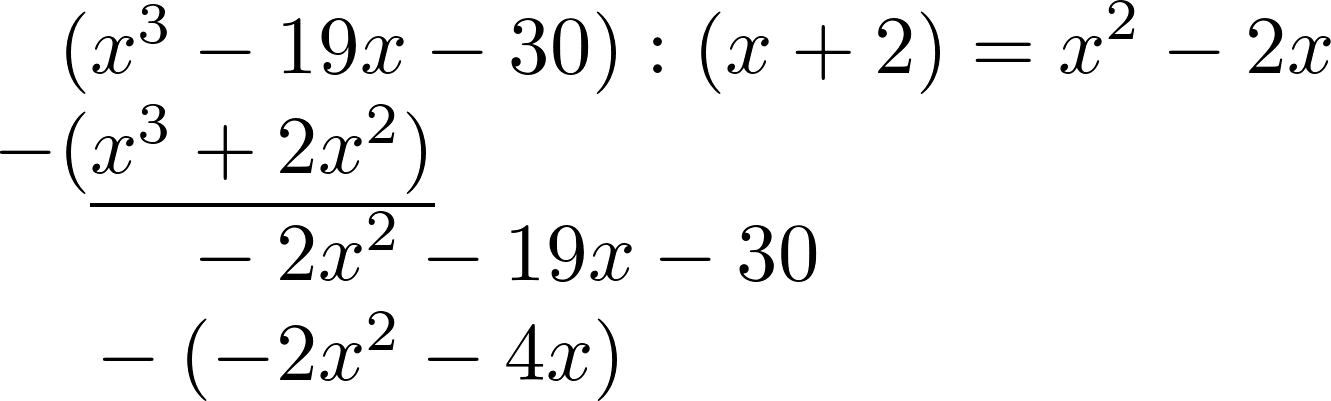
   Обе линии снова вычитаются.

   
   

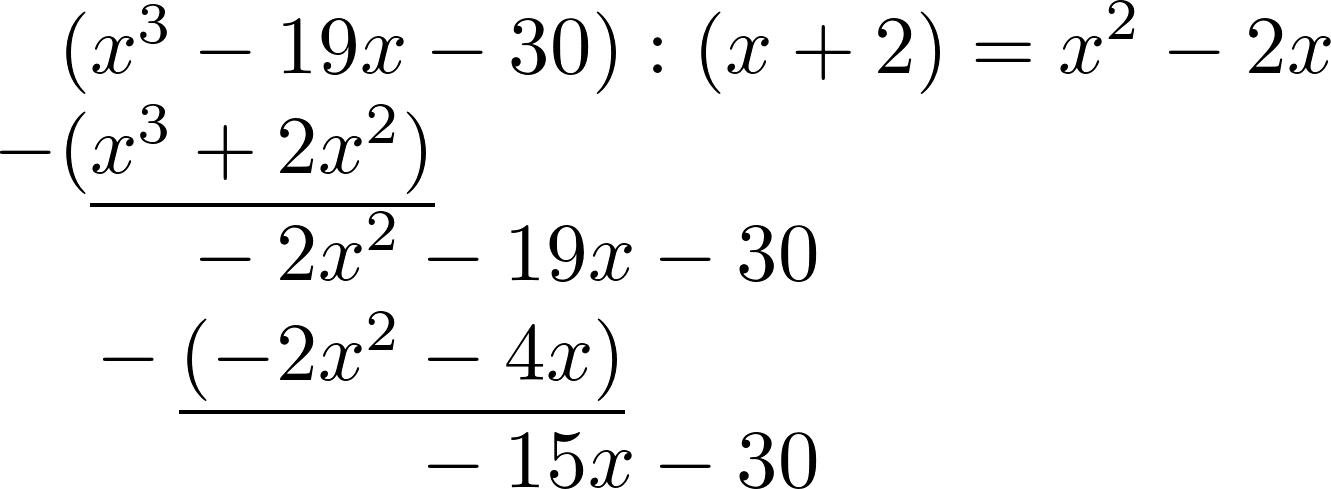
   В итоге, $-15x:x$ было вычислено, умножено и снова вычтено. Остаток 0; деление многочленов выполнено.

   
   

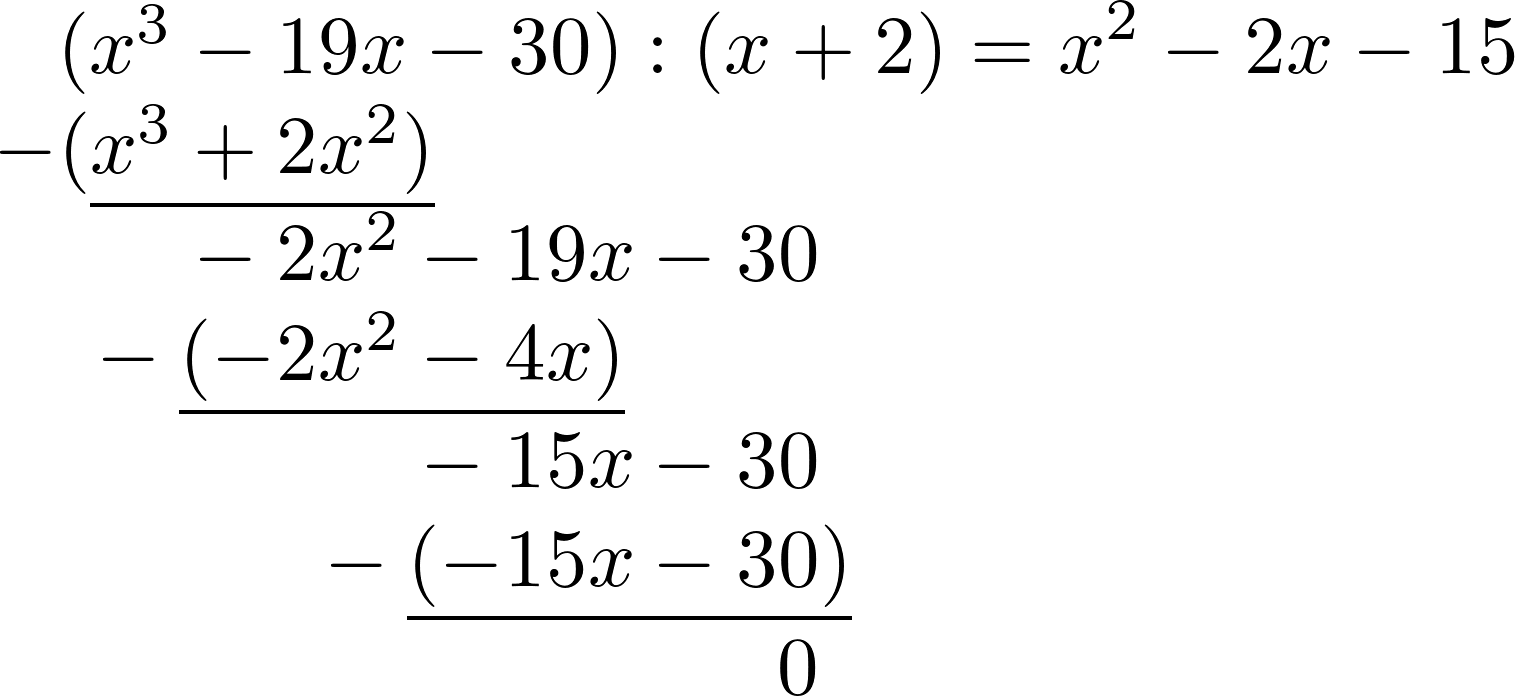
3. Решите квадратное уравнение

   Новое квадратное уравнение можно решить, например, используя pq-формулу.
   $x^2-2x-15=0$
   
   $x_{2,3} = \frac{p}{2} \pm\sqrt{(\frac{p}{2})^2-q}$
   
   $x_{2,3} = 1 \pm\sqrt{1^2+15}$
   $x_{2,3} = 1 \pm\sqrt{16}$
   $x_{2,3} = 1 \pm4$
   
   $x_2=5$ и $x_3=-3$
   
   Решения первоначального уравнения: $x_1=-2$, $x_2=5$ и $x_3=-3$