Abstand einer Geraden/Ebene zu einer parallelen Ebene
Als Abstand bezeichnet man die Länge der kürzesten Verbindung.
Wenn eine Gerade und Ebene parallel zueinander sind, dann haben sie einen konstanten Abstand.
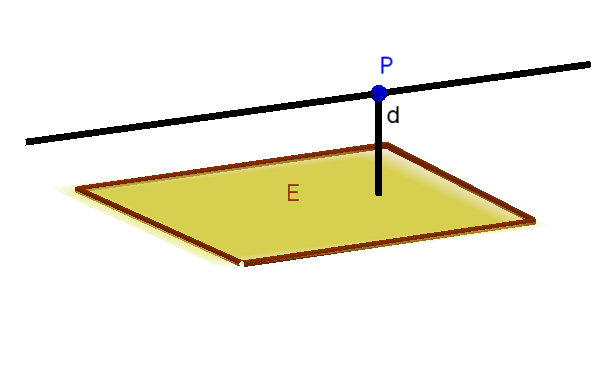
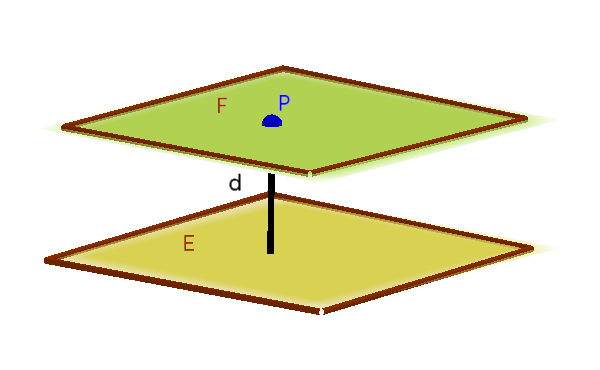
Ebenso verhält es sich mit zwei parallelen Ebenen.
Info
Wie man im Bild oben erkennt, ist der Abstand nichts anderes als der Abstand eines Punktes zur Ebene. Da beide parallel sind, kann ein beliebiger Punkt gewählt werden und in die HNF der Ebene eingesetzt werden.
Vorgehensweise
- Parallelität überprüfen
- Punkt (Stützpunkt) auswählen
- Hessesche Normalform aufstellen
- Punkt einsetzen
Beispiel (Gerade und Ebene)
$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$
$\text{E: } \left(\vec{x} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix}=0$
-
Parallelität überprüfen
Da der Abstand nur bei Parallelität berechnet werden kann, muss man überprüfen, ob die Gerade und Ebene parallel sind.
Um es möglichst einfach zu halten, wird geschaut ob der Normalenvektor der Ebene und der Richtungsvektor der Geraden othogonal zueinander sind. Das Skalarprodukt muss null sein.
$\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}\cdot\begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix}$ $=2-2+0$ $=0$
-
Punkt auswählen
Man kann jeden beliebigen Punkt der Gerade nehmen. Da man den Stützpunkt jedoch einfach ablesen kann, bietet sich dieser an.
$P(1|2|1)$
-
Hessesche Normalform aufstellen
$|\vec{n}|=\sqrt{2^2+(-2)^2+4^2}$ $=\sqrt{24}$
$\vec{n_0}= \frac{\vec{n}}{|\vec{n}|}$ $=\begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix}$
$\text{E: } \left(\vec{x} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix}=0$
-
Punkt einsetzen
$\vec{p}=\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}$
$d=$ $\left|\left(\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix} \right|$ $=\left|\begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix} \right|$ $=|-\frac4{\sqrt{24}}|$ $\approx0,82$
Beispiel (Ebene und Ebene)
$\text{F: } \left(\vec{x} - \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} -4 \\ 4 \\ -8 \end{pmatrix}=0$
$\text{E: } \left(\vec{x} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix}=0$
-
Parallelität überprüfen
Da der Abstand nur bei Parallelität berechnet werden kann, muss man überprüfen, ob die Ebenen parallel sind.
Dazu schauen wir, ob die Normalenvektoren parallel sind. Anders als bei der Gerade wird also nicht auf Rechtwinkligkeit überprüft.
$\vec{n_1}=r\cdot\vec{n_2}$
$\begin{pmatrix} -4 \\ 4 \\ -8 \end{pmatrix}=r\cdot\begin{pmatrix}2 \\ -2 \\ 4 \end{pmatrix}$ $\Rightarrow r=-2$
Es existiert ein $r$: Die Vektoren sind Vielfache voneinander und daher parallel.
-
Punkt auswählen
Man kann jeden beliebigen Punkt der Ebene nehmen. Da man den Stützpunkt jedoch einfach ablesen kann, bietet sich dieser an.
$P(1|2|1)$
-
Hessesche Normalform aufstellen
$|\vec{n}|=\sqrt{2^2+(-2)^2+4^2}$ $=\sqrt{24}$
$\vec{n_0}= \frac{\vec{n}}{|\vec{n}|}$ $=\begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix}$
$\text{E: } \left(\vec{x} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix}=0$
-
Punkt einsetzen
$\vec{p}=\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}$
$d=$ $\left|\left(\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix} \right|$ $=\left|\begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix} \right|$ $=|-\frac4{\sqrt{24}}|$ $\approx0,82$
