Abstand paralleler Geraden
Parallele Geraden haben überall einen konstanten Abstand.
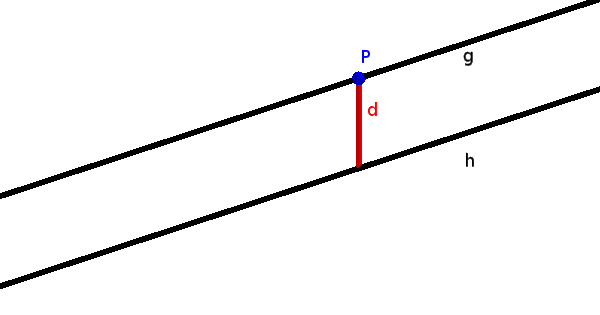
Info
Auch hier können wir uns einfach einen Punkt auf der einen Gerade aussuchen und den Abstand eines Punktes zur Gerade berechnen.
Vorgehensweise
- Parallelität überprüfen
- Punkt (Stützpunkt) auswählen
- Abstand des Punktes zur anderen Gerade
Beispiel
$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$
$\text{h: } \vec{x} = \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix}$
-
Parallelität überprüfen
Da diese Methode nur bei parallelen Geraden funktioniert, muss man überprüfen, ob die Geraden parallel sind.
Dazu schauen wir, ob die Richtungsvektoren kollinear (parallel) sind.
$\vec{a}=r\cdot\vec{b}$
$\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=r\cdot\begin{pmatrix}3 \\ 3 \\ 0 \end{pmatrix}$ $\Rightarrow r=3$
Es existiert ein $r$: Die Vektoren sind Vielfache voneinander und daher parallel.
-
Punkt auswählen
Man kann jeden beliebigen Punkt der Gerade nehmen. Da man den Stützpunkt jedoch einfach ablesen kann, bietet sich dieser an.
$P(-1|0|3)$
-
Abstand des Punktes zur anderen Geraden
Der Abstand kann nun wie unter Abstand Punkt und Gerade beschrieben berechnet werden.
Zuerst eine Hilfsebene mit $P$ als Stützpunkt und Richtungsvektor als Normalenvektor aufstellen.
$\text{H: } (\vec{x} - \vec{a}) \cdot \vec{n}=0$
$\text{H: } (\vec{x} - \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}) \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$
Der Lotfußpunkt ist der Schnittpunkt der Geraden $g$ und der Hilfsebene $H$. Zur Berechnung des Schnittpunkts wird die Geradengleichung für $\vec{x}$ in die Ebene eingesetzt.
$\left(\color{red}{\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}} - \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}\right)$ $\cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$
$\begin{pmatrix} 2+r \\ 2+r \\ -2 \end{pmatrix}$ $\cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$
Skalarprodukt berechnen
$(2+r)\cdot1+(2+r)\cdot1$ $+(-2)\cdot0=0$
$4+2r=0\quad|-4$
$2r=-4\quad|:2$
$r=-2$$r$ in $g$ einsetzen, um Lotfußpunkt $F$ zu erhalten
$\vec{OF} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \color{red}{-2} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$ $= \begin{pmatrix} 1-2 \\ 2-2 \\ 1-0 \end{pmatrix}$ $= \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}$
$F(-1|0|1)$
Der Abstand des Lotfußpunktes zum Punkt $P$ ist auch der Abstand der Geraden zu diesem Punkt.
Der Abstand zwischen zwei Punkten lässt sich einfach mit Vektoren berechnen.
$d=|\vec{PF}|$ $=\left| \begin{pmatrix} -1-(-1) \\ 0-0 \\ 1-3 \end{pmatrix}\right|$ $=\left| \begin{pmatrix} 0 \\ 0 \\ -2 \end{pmatrix}\right|$ $=\sqrt{(-2)^2}$ $=2$
Der Abstand der beiden Geraden $g$ und $h$ beträgt 2 LE.
