Расстояние между параллельными прямыми
Параллельные прямые имеют постоянное расстояние везде.
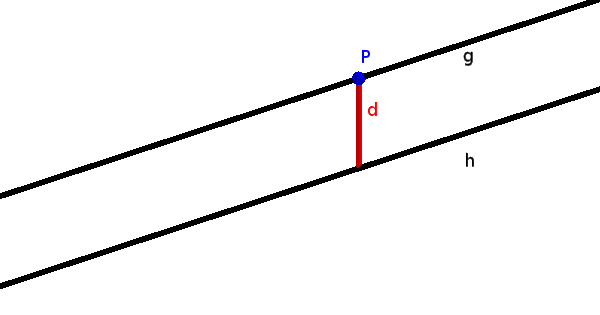
Информация
Здесь мы также можем просто выбрать точку на линии и рассчитать рассточние между точкой и прямой.
Например
$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$
$\text{h: } \vec{x} = \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix}$
-
Проверьте параллелизм
Поскольку этот метод работает только с параллельными линиями, вы должны проверить, являются ли эти прямые параллельными.
Мы смотрим, являются ли векторы направления коллинеарными (параллельными).
$\vec{a}=r\cdot\vec{b}$
$\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=r\cdot\begin{pmatrix}3 \\ 3 \\ 0 \end{pmatrix}$ $\Rightarrow r=3$
Существует $r$: векторы кратны друг другу и, следовательно, параллельны.
-
Выбранная точка
Вы можете взять любую точку на прямой. Однако, поскольку вы можете легко прочитать точку поддержки, это хороший вариант.
$P(-1|0|3)$
-
Расстояние от точки до другой прямой
Расстояние теперь можно рассчитать, как описано в разделе,расстояние точки и прямой.
Сначала установите вспомогательную плоскость с $P$ в качестве опорной точки и вектора направления, в качестве нормального вектора.
$\text{H: } (\vec{x} - \vec{a}) \cdot \vec{n}=0$
$\text{H: } (\vec{x} - \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}) \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$
Перпендикулярная точка - это пересечение прямой $g$ и вспомогательной плоскости $H$. Для вычисления пересечения используется уравнение прямой для $\vec{x}$ на плоскости.
$\left(\color{red}{\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}} - \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}\right)$ $\cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$
$\begin{pmatrix} 2+r \\ 2+r \\ -2 \end{pmatrix}$ $\cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$
Вычислите скалярное произведение
$(2+r)\cdot1+(2+r)\cdot1$ $+(-2)\cdot0=0$
$4+2r=0\quad|-4$
$2r=-4\quad|:2$
$r=-2$Вставьте $r$ в $g$, чтобы получить перпендикулярную точку $F$.
$\vec{OF} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \color{red}{-2} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$ $= \begin{pmatrix} 1-2 \\ 2-2 \\ 1-0 \end{pmatrix}$ $= \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}$
$F(-1|0|1)$
Расстояние от перпендикулярной точки до точки $P$ также является расстоянием от прямой до этой точки.
Расстояние между двумя точками можно легко вычислить с помощью векторов.
$d=|\vec{PF}|$ $=\left| \begin{pmatrix} -1-(-1) \\ 0-0 \\ 1-3 \end{pmatrix}\right|$ $=\left| \begin{pmatrix} 0 \\ 0 \\ -2 \end{pmatrix}\right|$ $=\sqrt{(-2)^2}$ $=2$
Расстояние между двумя прямыми $g$ и $h$ составляет 2 LU.
