Расстояние от прямой / плоскости до параллельной плоскости
Расстояние - это длина самого короткого соединения.
Если прямая и плоскость параллельны друг другу, то они находятся на постоянном расстоянии.
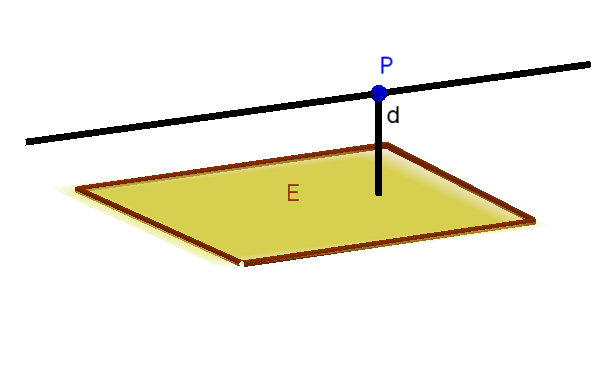
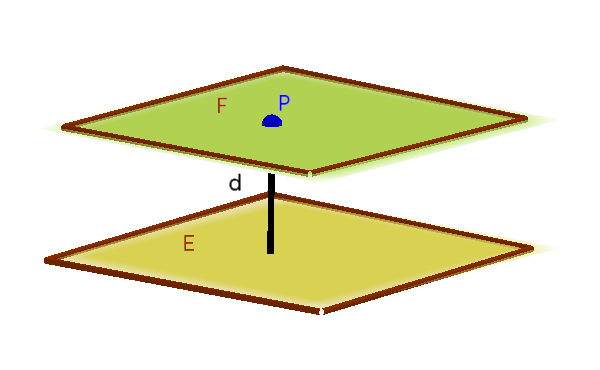
То же самое относится и к двум параллельным плоскостям .
Информация
Как вы можете видеть на картинке выше, расстояние - это не что иное, как расстояние точки до плоскости. Поскольку обе они параллельны, любая точка может быть выбрана и вставлена в нормальную формулу плоскости Гессе.
Метод
- Проверка параллельности
- Выберите точку (точка опоры)
- Составьте нормальную формулу Гессе
- Вставьте точку
Например (прямая и плоскость)
$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$
$\text{E: } \left(\vec{x} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix}=0$
-
Проверка параллельности
Поскольку расстояние может быть вычислено только при наличии параллелизма, вы должны проверить, есть ли параллельная прямая и плоскость .
Чтобы сделать его как можно более простым, мы рассмотрим, являются ли нормальный вектор плоскости и вектор направления прямой ортогональными друг другу. Скалярное произведение должно быть равно нулю.
$\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}\cdot\begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix}$ $=2-2+0$ $=0$
-
Выбранная точка
Вы можете взять любую точку на прямой. Однако, так как вы можете легко найти точку поддержки, Это хороший вариант.
$P(1|2|1)$
-
Составьте нормальную формулу Гессе
$\vec{n_0}= \frac{\vec{n}}{|\vec{n}|}$ $=\begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix}$
$\text{E: } \left(\vec{x} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix}=0$
-
Вставьте точку
$\vec{p}=\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}$
$d=$ $\left|\left(\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix} \right|$ $=\left|\begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix} \right|$ $=|-\frac4{\sqrt{24}}|$ $\approx0.82$
Например (плоскость и плоскость)
$\text{F: } \left(\vec{x} - \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} -4 \\ 4 \\ -8 \end{pmatrix}=0$
$\text{E: } \left(\vec{x} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix}=0$
-
Проверка параллельности
Поскольку расстояние может быть вычислено только при наличии параллелизма, вы должны проверить, есть ли параллельная плоскость .
Мы посмотрим, параллельны ли нормальные векторы.
$\vec{n_1}=r\cdot\vec{n_2}$
$\begin{pmatrix} -4 \\ 4 \\ -8 \end{pmatrix}=r\cdot\begin{pmatrix}2 \\ -2 \\ 4 \end{pmatrix}$ $\Rightarrow r=-2$
Существует $r$: векторы кратны друг другу и, следовательно, параллельны..
-
Выбранная точка
Вы можете взять любую точку на плоскости. Однако, поскольку вы можете легко найти точку поддержки, это хороший вариант.
$P(1|2|1)$
-
Составьте нормальную формулу Гессе
$|\vec{n}|=\sqrt{2^2+(-2)^2+4^2}$ $=\sqrt{24}$
$\vec{n_0}= \frac{\vec{n}}{|\vec{n}|}$ $=\begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix}$
$\text{E: } \left(\vec{x} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix}=0$
-
Вставьте точку
$\vec{p}=\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}$
$d=$ $\left|\left(\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} - \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\right) \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix} \right|$ $=\left|\begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 2/\sqrt{24} \\ -2/\sqrt{24} \\ 4/\sqrt{24} \end{pmatrix} \right|$ $=|-\frac4{\sqrt{24}}|$ $\approx0.82$
