Math ↠ Distance calculations ↠ Parallel lines

Distance between parallel lines

Parallel lines have a constant distance everywhere.

i

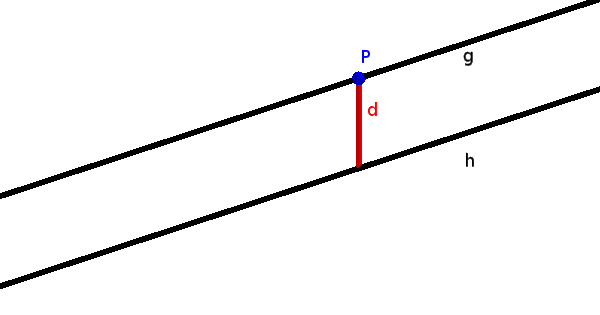
Info

Intersecting and coincident lines have a distance of 0. Distance calculation is possible with skew and parallel lines.

Here, too, we can simply choose a point on a line and calculate the distance between a point and the straight line.

i

Method

  1. Check parallelism
  2. Select point (support point)
  3. Distance of the point to the other line

Example

$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$

$\text{h: } \vec{x} = \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix}$

  1. Check parallelism

    Since this method only works with parallel lines, you have to check whether the lines are parallel.

    We look at whether the direction vectors are collinear (parallel).

    $\vec{a}=r\cdot\vec{b}$

    $\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=r\cdot\begin{pmatrix}3 \\ 3 \\ 0 \end{pmatrix}$ $\Rightarrow r=3$

    There is an $r$: The vectors are multiples of one another and therefore parallel.

  2. Select point

    You can take any point on the line. However, since you can easily read off the support point, this is a good option.

    $P(-1|0|3)$

  3. Distance of the point to the other line

    The distance can now be calculated as described under distance point and line.

    First set up an auxiliary plane with $P$ as the support point and direction vector as the normal vector.

    $\text{H: } (\vec{x} - \vec{a}) \cdot \vec{n}=0$

    $\text{H: } (\vec{x} - \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}) \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$

    The perpendicular point is the intersection of the line $g$ and the auxiliary plane $H$. To calculate the intersection, the equation of a line for $\vec{x}$ is used in the plane.

    $\left(\color{red}{\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}} - \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}\right)$ $\cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$

    $\begin{pmatrix} 2+r \\ 2+r \\ -2 \end{pmatrix}$ $\cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$

    Calculate scalar product

    $(2+r)\cdot1+(2+r)\cdot1$ $+(-2)\cdot0=0$
    $4+2r=0\quad|-4$
    $2r=-4\quad|:2$
    $r=-2$

    Insert $r$ in $g$ to get perpendicular point $F$.

    $\vec{OF} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \color{red}{-2} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$ $= \begin{pmatrix} 1-2 \\ 2-2 \\ 1-0 \end{pmatrix}$ $= \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}$


    $F(-1|0|1)$

    The distance from the perpendicular point to point $P$ is also the distance from the line to this point.

    The distance between two points can be easily calculated using vectors.

    $d=|\vec{PF}|$ $=\left| \begin{pmatrix} -1-(-1) \\ 0-0 \\ 1-3 \end{pmatrix}\right|$ $=\left| \begin{pmatrix} 0 \\ 0 \\ -2 \end{pmatrix}\right|$ $=\sqrt{(-2)^2}$ $=2$

    The distance between the two lines $g$ and $h$ is 2 LU.