Mathe ↠ Ableitung anwenden ↠ Tangentengleichung

Tangentengleichung

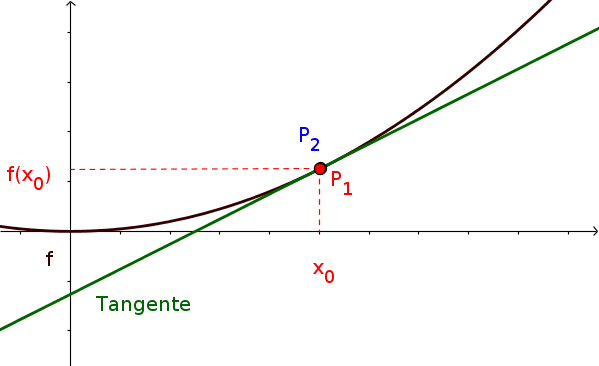
Auch beim Aufstellen der Tangentengleichung eines Punktes nutzt man die Ableitung. Als Tangente bezeichnet man eine Gerade, die an genau einem Punkt des Graphen anliegt und ihre Steigung dem Differenzialquotienten entspricht.

Tangente an einem Punkt
!

Merke

Die Gleichung der Tangenten an der Stelle $x$ ist:
$t(x)=mx+n$
Die Steigung der Tangenten kann man mit der Ableitung an der Stelle $x$ bestimmen:
$m=f'(x)$
i

Vorgehensweise

  1. Ableitung bestimmen
  2. Steigung berechnen
  3. Steigung einsetzen
  4. $n$ berechnen und einsetzen

Beispiel

Gib die Tangentengleichung der Funktion $f(x)=-x^2+3$ an der Stelle $x=2$ an.

  1. Ableitung bestimmen

    Stammfunktion: $f(x)=-x^2+3$
    Ableitung: $f'(x)=-2x$

  2. Steigung berechnen

    $f'(2)=-2\cdot2=-4$

  3. Steigung einsetzen

    $t(x)=mx+n$

    $m=f'(2)=-4$
    $t(x)=-4x+n$

  4. $n$ berechnen und einsetzen

    Die Tangente geht durch den Punkt $P(2|f(2))$. Um $n$ zu berechnen, wird der Punkt in die Gleichung eingesetzt
    $f(2)=-2^2+3=-1$
    => $P(\color{blue}{2}|\color{green}{-1})$

    $t(x)=-4x+n$
    $\color{green}{-1}=-4\cdot\color{blue}{2}+n$
    $-1=-8+n\quad|+8$
    $n=7$

    $t(x)=-4x+7$

Tangentengleichung aufstellen, Tangente an Kurve

Kooperation mit dem Kanal von Mister Mathe

Mit dem Abspielen dieses Videos akzeptierst du YouTubes Datenschutzerklärung.

Videos von YouTube immer laden

Bei der Tangenten handelt es sich um den Graphen einer linearen Funktion. Die Funktionsgleichung besteht also aus einer Steigung $m$ und dem y-Achsenabschnitt $n$:

$y=mx+n$

Meistens hat man einen Punkt $P(x|y)$ und eine Funktion $f$ gegeben. Die Steigung kann durch Einsetzen von $x$ in die Ableitung $f'$ berechnet werden. Anschließend wird der y-Achsenabschnitt bestimmt, indem man den Punkt $P$ in die Gleichung einsetzt und nach $n$ auflöst.