Berührpunkte
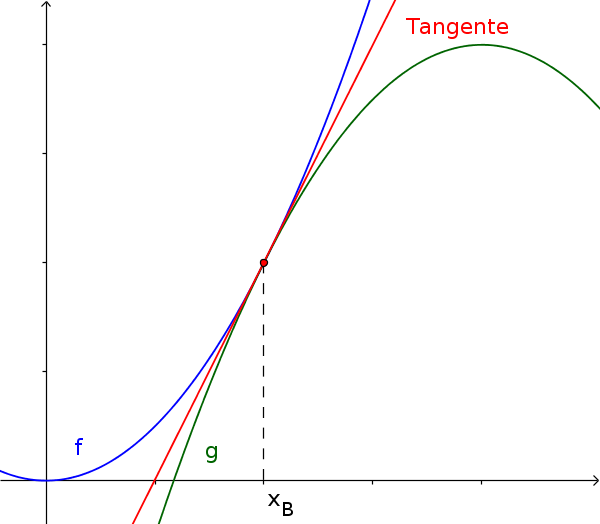
Ein Berührpunkt ist ein gemeinsamer Punkt von zwei Funktionsgraphen, an dem beide Funktionen dieselbe Tangente (gleiche Steigung) besitzen.
!
Merke
Zwei Funktionen besitzen einen Berührpunkt, wenn gilt:
$f(x_B)=g(x_B)$ und
$f'(x_B)=g'(x_B)$
$f(x_B)=g(x_B)$ und
$f'(x_B)=g'(x_B)$
i
Vorgehensweise
- Ableitungen bilden
- Funktionsgleichungen gleichsetzen: $f(x_B)=g(x_B)$
- Steigungen überprüfen
- Berührpunkt angeben
Beispiel
Bestimme den Berührpunkt der Funktion $f(x)=x^2$ und $g(x)=-x^2+4x-2$.
Ableitungen bilden
$f(x)=x^2$
$f'(x)=2x$
$g(x)=-x^2+4x-2$
$g'(x)=-2x+4$-
Funktionsgleichungen gleichsetzen
Erste Bedingung: Beide Funktionen müssen einen gemeinsamen Punkt besitzen.
$f(x_B)=g(x_B)$
$x^2=-x^2+4x-2\quad|-x^2$
$-2x^2+4x-2=0\quad|:(-2)$
$x^2-2x+1=0$
Es liegt eine quadratische Gleichung vor, die man beispielsweise mit der PQ-Formel lösen kann.
$x_{B_{1,2}} = -\frac{p}{2} \pm\sqrt{(\frac{p}{2})^2-q}$
$x_{B_{1,2}} = 1 \pm\sqrt{1-1}$
$x_B=\color{red}{1}$ -
Steigung überprüfen
Zweite Bedingung: Beide Funktionen müssen an dem Punkt die gleiche Steigung besitzen.
$f'(x_B)=g'(x_B)$
$f'(\color{red}{1})=g'(\color{red}{1})$
$2\cdot\color{red}{1}=-2\cdot\color{red}{1}+4$
$2=2$
=> die Funktionen berühren sich an der Stelle $x_B=1$ -
Berührpunkt angeben
Es soll der BerührPUNKT angegeben werden: Deshalb noch die y-Koordinate mit einer der ursprünglichen Funktionen berechnen.
$f(\color{red}{1})=\color{red}{1}^2=\color{blue}{1}$
=> Berührpunkt: $B(\color{red}{1}|\color{blue}{1})$
Berührpunkte von Funktionen, Ableitung, Differenzialrechnung, gemeinsamer Punkt, Tangente, Steigung
Kooperation mit dem Kanal von Mister Mathe
Ein Berührpunkt ist eine besondere Art von Schnittpunkt, da dort nicht nur die Funktionswerte sondern auch die Steigungen übereinstimmen.
Um die Berührpuntke zu finden, muss man also zuerst die Schittpunkte bestimmen und dann mithilfe der Ableitungen auf das zweite Kriterium $f'(x)=g'(x)$ prüfen. Wenn nicht nur die Berührstelle sondern der Berührpunkt gefragt ist, muss man ebenfalls immer die y-Koordinate mit einer der beiden Ausgangsfunktionen ausrechnen.

