Schnittwinkel
Wenn sich die Graphen von zwei Funktionen schneiden, bilden die Tangenten zwei Winkel miteinander. Der kleinere Winkel wird als Schnittwinkel bezeichnet.
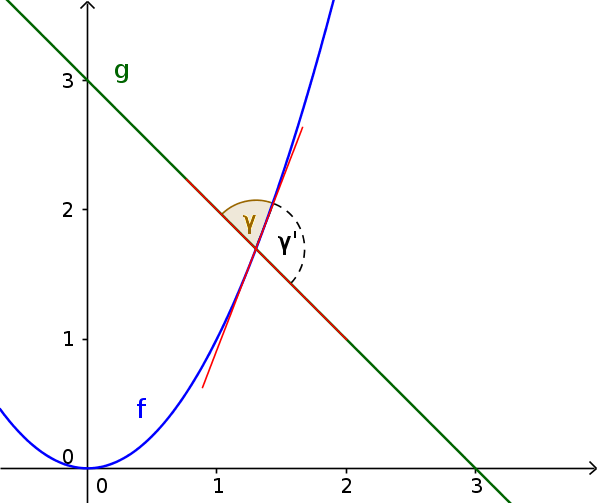
Zum Bild: Durch das Schneiden der beiden Tangenten (rot) bilden sich zwei Winkel: $\gamma$ und $\gamma'$.
$\gamma$ ist der Schnittwinkel.
Merke
Zuerst benötigt man die Steigungswinkel der Funktionen:
$\alpha=\arctan(f'(x))$
$\beta=\arctan(g'(x))$
Der Schnittwinkel ist der kleinere Wert:
$|\alpha-\beta|$ oder
$180^\circ-|\alpha-\beta|$
Vorgehensweise
- Ableitungen bilden
- Steigungen berechnen
- Steigungswinkel berechnen
- Schnittwinkel angeben
Beispiel
Wie groß ist der Schnittwinkel von den Funktionen $f(x)=x^2$ und $g(x)=x+2$ am Schnittpunkt $P(2|4)$.
Ableitungen bilden
$f(x)=x^2$
$f'(x)=2x$
$g(x)=x+2$
$g'(x)=1$Steigungen berechnen
Es wird die Steigung der beiden Funktionen am Schnittpunkt berechnet ($x=2$).
$f'(2)=2\cdot2=4$
$g'(2)=1$Steigungswinkel berechnen
$\alpha=\arctan(f'(x))$
$\alpha=\arctan(4)\approx75,96°$
$\beta=\arctan(g'(x))$
$\beta=\arctan(1)=45°$-
Schnittwinkel angeben
$\gamma_1=|\alpha-\beta|$
$\gamma_1=|75,96°-45°|$ $=30,96°$
$\gamma_2=180°-|\alpha-\beta|$
$\gamma_2=180°-30,96°$ $=149,04°$
$\gamma_1<\gamma_2$
=> der Schnittwinkel $\gamma$ beträgt $30,96°$
Schnittwinkel zwischen Funktionen, Schnittwinkel, Steigung, Steigunswinkel, alpha, beta, gamma
Voraussetzung für das Vorhandensein eines Schnittwinkels ist, dass sich die beiden Funktionen schneiden. Für jeden Schnittpunkt lässt sich dann der Schnittwinkel bestimmen.
Sollte kein Schnittpunkt gegeben sein, müssen die beiden Funktionen erstmal gleich gesetzt werden, um diesen zu bestimmen. An diesem können für beide Funktionen die Steigungswinkel $\alpha$ und $\beta$ berechnet werden.
Am Schnittpunkt finden sich zwei Winkel, wobei nur der kleinere als Schnittwinkel bezeichnet wird:

