Math ↠ Derivative applications ↠ Angle of intersection

Angle of intersection

When the graphs intersect with two functions, the tangents form two angles with each other. The smaller angle is called the angle of intersection.


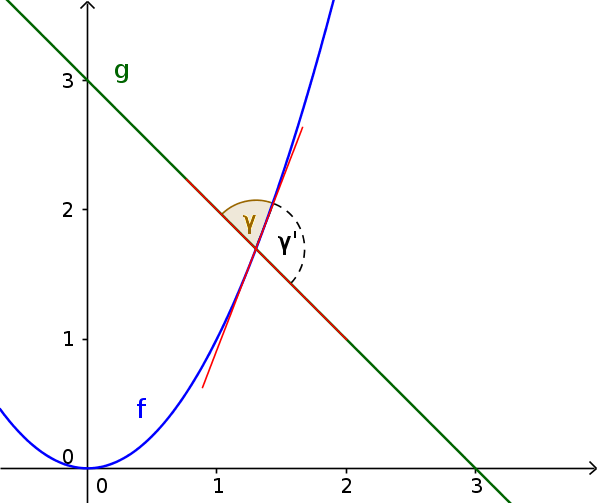
The picture: By cutting the two tangents (red) two angles are formed: $\gamma$ and $\gamma'$.
$\gamma$ is the angle of intersection.


!

Remember

$f$ and $g$ intersect at point $x$.

First, you need the slope angles of the functions:
$\alpha=\arctan(f'(x))$
$\beta=\arctan(g'(x))$

The angle of intersection has the smaller value:
$|\alpha-\beta|$ or
$180^\circ-|\alpha-\beta|$
i

Method

  1. Take derivatives
  2. Calculate slopes
  3. Calculate slope angle
  4. Specify the angle of intersection

Example

What is the angle of intersection of the functions $f(x)=x^2$ and $g(x)=x+2$ at the intersection $P(2|4)$.

  1. Take derivatives

    $f(x)=x^2$
    $f'(x)=2x$

    $g(x)=x+2$
    $g'(x)=1$

  2. Calculate slopes

    The slope of the two functions at the intersection is calculated ($x=2$).
    $f'(2)=2\cdot2=4$
    $g'(2)=1$

  3. Calculate slope angle

    $\alpha=\arctan(f'(x))$
    $\alpha=\arctan(4)\approx75.96°$

    $\beta=\arctan(g'(x))$
    $\beta=\arctan(1)=45°$

  4. Specify the angle of intersection

    $\gamma_1=|\alpha-\beta|$
    $\gamma_1=|75.96°-45°|$ $=30.96°$

    $\gamma_2=180°-|\alpha-\beta|$
    $\gamma_2=180°-30.96°$ $=149.04°$

    $\gamma_1<\gamma_2$
    => The angle of intersection $\gamma$ is $30.96°$