Математика ↠ Производные положения ↠ Угол пересечения

Угол пересечения

Когда графики пересекаются с двумя функциями, касательные образуют два угла друг с другом. Меньший угол называется углом пересечения.


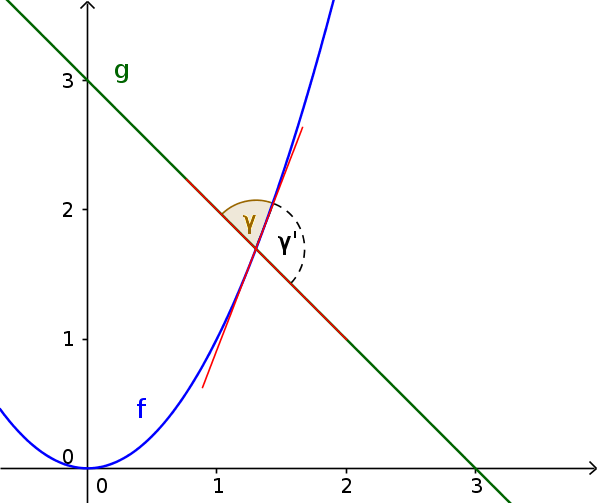
Рисунок: Путем разрезания двух касательных (красных) образуются два угла: $\gamma$ и $\gamma'$.
$\gamma$ - угол пересечения.


!

Запомни

$f$ и $g$ пересекается в точке $x$.

Во-первых, вам нужен угол наклона функции:
$\alpha=\arctan(f'(x))$
$\beta=\arctan(g'(x))$

Угол пересечения имеет меньшее значение:
$|\alpha-\beta|$ или
$180^\circ-|\alpha-\beta|$
i

Способ

  1. Берете производную
  2. Вычисляете наклоны
  3. Вычисляете угол наклона
  4. Определяем угол пересечения

Пример

Определите угол пересечения функций $f(x)=x^2$ и $g(x)=x+2$ в точке пересечения $P(2|4)$.

  1. Берем производную

    $f(x)=x^2$
    $f'(x)=2x$

    $g(x)=x+2$
    $g'(x)=1$

  2. Вычисляем наклон

    Подсчитываем наклон двух функций ($x=2$).
    $f'(2)=2\cdot2=4$
    $g'(2)=1$

  3. Вычисляем угол наклона

    $\alpha=\arctan(f'(x))$
    $\alpha=\arctan(4)\approx75.96°$

    $\beta=\arctan(g'(x))$
    $\beta=\arctan(1)=45°$

  4. Определяем угол пересечения

    $\gamma_1=|\alpha-\beta|$
    $\gamma_1=|75.96°-45°|$ $=30.96°$

    $\gamma_2=180°-|\alpha-\beta|$
    $\gamma_2=180°-30.96°$ $=149.04°$

    $\gamma_1<\gamma_2$
    => Угол пересечения $\gamma$ равен $30.96°$