Kurvendiskussion
Die Differenzialrechnung wird bei der Kurvendiskussion benötigt. Hier folgt nur nochmal eine kurze Zusammenfassung.
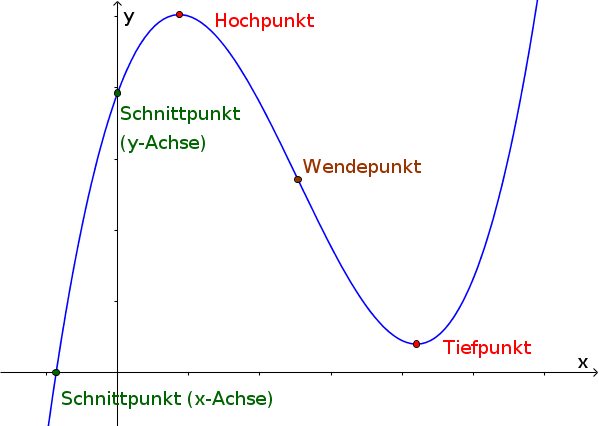
Eine Kurvendiskussion beinhaltet meist folgende Untersuchungen:
| Eigenschaft | Bedingung | |
|---|---|---|
| Achsenschnittpunkte | ||
| Schnittstellen x-Achse (Nullstellen) | $f(x)=0$ | |
| Schnittstelle y-Achse | $f(0)$ berechnen | |
| Symmetrie | ||
| Achsensymmetrie zur y-Achse | $f(-x)=f(x)$ | |
| Punktsymmetrie zum Ursprung | $f(-x)=-f(x)$ | |
| Monotonieverhalten | ||
| monoton steigend | $f'(x)\ge0$ | |
| monoton fallend | $f'(x)\le0$ | |
| streng monoton steigend | $f'(x)>0$ | |
| streng monoton fallend | $f'(x)<0$ | |
| Extrempunkte | ||
| Hochpunkt | $f'(x_E)=0$ und $f''(x_E)<0$ | |
| Tiefpunkt | $f'(x_E)=0$ und $f''(x_E)>0$ | |
| Wendepunkte | ||
| Wendepunkt | $f''(x_W)=0$ und $f'''(x_W)\neq0$ | |
Kurvendiskussion: Übersicht, Extrempunkte, Wendepunkte, Krümmung, Monotonie, Nullstellen
Kooperation mit dem Kanal von Mister Mathe
Die Kurvendiskussion ist ein Teilgebiet der Differenzialrechnung und steht in starkem Zusammenhang mit der Ableitung, mit deren Hilfe sich viele Eigenschaften ermitteln lassen. Für eine vollständige Kurvenuntersuchung werden zumindest die ersten drei Ableitungen der zu betrachtenden Funktion benötigt. Es bietet sich also an, diese zum Beginn alle aufzustellen.

