Extremalprobleme

Ein Aufgabentyp, bei dem die Differenzialrechnung zur Anwendung kommt, sind die Optimierungs- oder auch Extremalprobleme.

Beispiel

Es soll ein möglichst großes rechteckiges Gebiet mit 800m Zaun eingegrenzt werden. Berechne die Größe der beiden Seiten und des Flächeninhalts.

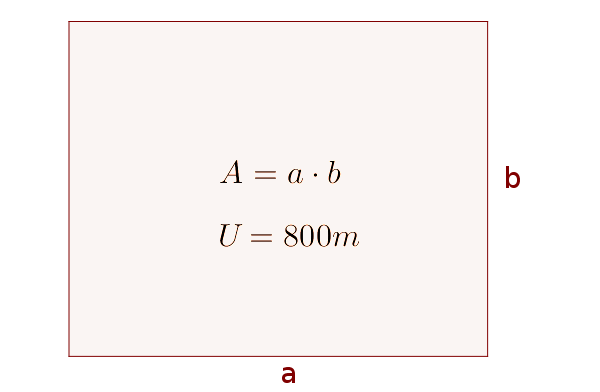
1. Hauptbedingung

   Die Fläche des Rechtecks soll maximal werden. Daher ist das die Hauptbedingung und abhängig von zwei Variablen $a$ und $b$.
   
   $A(a, b)=a\cdot b$

2. Nebenbedingung

   Es stehen nur 800m Zaun zur Verfügung, der das Gebiet eingrenzt. Dieser ist der Umfang des Rechtecks.
   
   $U=2a+2b$
   $800=2a+2b$

3. Zielfunktion aufstellen

   Um beide Bedingungen miteinander zu verknüpfen, wird die Nebenbedingung nach einer Variablen umgestellt.
   $800=2a+2b\quad|-2b$
   $800-2b=2a\quad|:2$
   $a=\frac{800-2b}2$ $=400-b$
   
   Jetzt muss das in die Hauptbedingung eingesetzt werden und man erhält die Zielfunktion, die nur noch von einer Variablen abhängig ist.
   $A(a, b)=a\cdot b$
   $A(b)=(400-b)\cdot b$ $=400b-b^2$

4. Extremwerte der Zielfunktion berechnen

   Nun kann man (wie bei anderen Funktionen auch) die Extremwerte der Zielfunktion berechnen.
   $A(b)=400b-b^2$
   $A'(b)=400-2b$
   
   $400-2b=0\quad|-400$
   $-2b=-400\quad|:(-2)$
   $b=200$
   
   Mit der zweiten Ableitung überprüft man noch, ob das Ergebnis tatsächlich ein Hochpunkt ist, da der Flächeninhalt maximal werden soll.
   $A''(b)=-2$
   $A''(200)=-2<0$ => Hochpunkt
   

5. Berechnen fehlender Größen

   $b=200m$
   
   Aus der (umgestellten) Nebenbedingung kann man nun $a$ berechnen.
   $a=400-b$
   $a=400-200=200m$
   
   Aus der Hauptbedingung (alternativ auch mit der Zielfunktion) lässt sich der Flächeninhalt $A$ berechnen.
   $A(a, b)=a\cdot b$
   $A(a, b)=200m\cdot 200m=40.000m^2$