Задачи на экстремум

Тип задач, в котором используются различные исчисления - оптимизационные или задачи на экстремум. Задача на экстремум - это своего рода задача оптимизации, но только с одним ограничением. Это может быть как максимизация, так и минимизация.

Пример

Наибольшая прямоугольная область должна быть ограничена 800 м забором. Вычислите размеры обеих сторон и площадь.

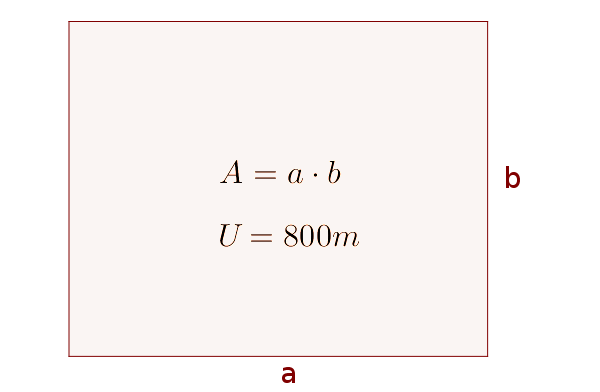
1. Основное условие

   Площадь прямоугольника следует максимизировать. Поэтому, это основное условие и оно зависит от двух переменных $a$ и $b$.
   
   $A(a, b)=a\cdot b$

2. Ограничение

   Нам доступно только 800м забора, что ограничивает область. Это является периметром прямоугольника.
   
   $P=2a+2b$
   $800=2a+2b$

3. Устанавливаем целевую функцию

   Чтобы связать оба условия, меняем ограничение на переменную.
   $800=2a+2b\quad|-2b$
   $800-2b=2a\quad|:2$
   $a=\frac{800-2b}2$ $=400-b$
   
   Теперь ипользуем это в основном условии и мы получаем целевую функцию, которая зависит только от одной переменной.
   $A(a, b)=a\cdot b$
   $A(b)=(400-b)\cdot b$ $=400b-b^2$

4. Вычисление экстремумов целевой функции

   Теперь мы можем (как и с другими функциями) вычислить экстремумы целевой функции.
   $A(b)=400b-b^2$
   $A'(b)=400-2b$
   
   $400-2b=0\quad|-400$
   $-2b=-400\quad|:(-2)$
   $b=200$
   
   Со второй деривацией (производной), еще нужно проверить, является ли результат максимальным, т.к. площадь должна быть максимумом.
   $A''(b)=-2$
   $A''(200)=-2<0$ => Максимум
   

5. Вычисление недостающих параметров

   $b=200m$
   
   Из (преобразованного) ограничения можно вычислить $a$.
   $a=400-b$
   $a=400-200=200m$
   
   Исходя из основного условия (альтернативно из целевой функции) площадь $A$ можно вычислить.
   $A(a, b)=a\cdot b$
   $A(a, b)=200m\cdot 200m=40.000m^2$