Streifenmethode
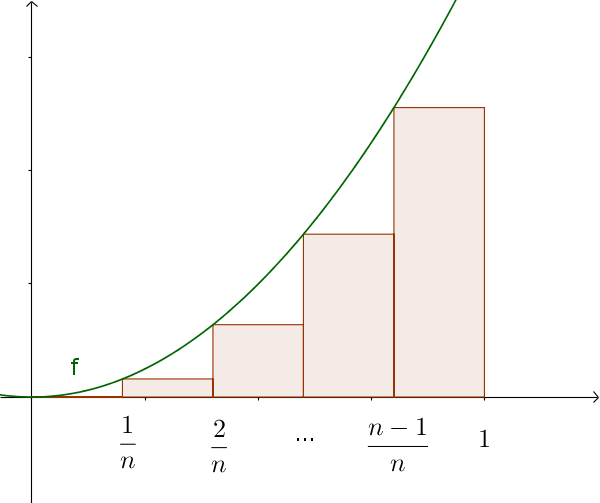
Wenn man nun die Streifenzahl $n$ gegen unendlich laufen lässt, erhält man also den gesuchten Flächeninhalt. Dazu bildet man den Grenzwert der Ober- und Untersummen für $n\to\infty$.
Beispiel
$f(x)=x^2$ im Intervall $[0; 1]$
-
Untersumme berechnen
Die Breite ist $\frac1n$ und die Höhe ist $x^2$.
$U=\frac1n\cdot(0^2+(\frac1n)^2+(\frac2n)^2+...$ $+(\frac{n-1}{n})^2)$
Klammern auflösen, indem man Zähler und Nenner quadriert.
$U=\frac1n\cdot(0^2+\frac{1^2}{n^2}+\frac{2^2}{n^2}+...$ $+\frac{(n-1)^2}{n^2})$
In jedem Nenner steht $n^2$, daher kann man das Ausklammern
$U=\frac{1}{n^3}\cdot(0^2+1^2+2^2+...+(n-1)^2)$
Es gibt einen Trick, um die Klammer umzuschreiben: Alle Quadratzahlen bis $m$ (sprich $1^2+2^2+...+m^2$) ergeben zusammen:
$\frac16\cdot\color{red}{m}\cdot(\color{red}{m}+1)\cdot(2\color{red}{m}+1)$
Auf unser Beispiel angewendet bedeutet das:
$\color{red}{m}=\color{red}{(n-1)}$
$U=\frac{1}{n^3}\cdot\frac16\cdot\color{red}{(n-1)}\cdot$ $(\color{red}{n-1}+1)\cdot(2\color{red}{(n-1)}+1)$
$U=\frac16\cdot\frac{1}{n^3}\cdot(n-1)\cdot n\cdot(2n-1)$ -
Obersumme berechnen
Das gleiche nochmal für die Obersumme.
$O=\frac1n\cdot((\frac1n)^2+(\frac2n)^2+...$ $+(\frac{n-1}{n})^2+1^2)$
$O=\frac{1}{n^3}\cdot(1^2+2^2+...$ $+(n-1)^2+n^2)$
$O=\frac16\cdot\frac{1}{n^3}\cdot n\cdot (n+1)\cdot(2n+1)$ -
Grenzwert bilden
Jetzt muss noch der Grenzwert gebildet werden.
$U=\frac16\cdot\frac{1}{n^3}\cdot(n-1)\cdot n\cdot(2n-1)$ $=\frac16\cdot\frac{n-1}{n}\cdot \frac{n}{n}\cdot \frac{2n-1}{n}$
$\lim\limits_{n \to \infty}{U}=$ $\lim\limits_{n \to \infty}{(\frac16\cdot\frac{n-1}{n}\cdot \frac{n}{n}\cdot \frac{2n-1}{n})}$ $=\frac16\cdot1\cdot1\cdot2=\frac13$
$O=\frac16\cdot\frac{1}{n^3}\cdot n\cdot (n+1)\cdot(2n+1)$ $=\frac16\cdot\frac{n}{n}\cdot\frac{n+1}{n}\cdot\frac{2n+1}{n}$
$\lim\limits_{n \to \infty}{O}=$ $\lim\limits_{n \to \infty}{(\frac16\cdot\frac{n}{n}\cdot\frac{n+1}{n}\cdot\frac{2n+1}{n})}$ $=\frac16\cdot1\cdot1\cdot2=\frac13$ -
Flächeninhalt bestimmen
Für den Flächeninhalt gilt:
$U \le A \le O$
$\frac13 \le A \le \frac13$
Der gesuchte Flächeninhalt ist also: $A=\frac13$
Streifenmethode zur Flächenberechnung, Integralrechnung, Obersumme, Untersumme, Integration, Fläche
Der Flächeninhalt unterhalb einer Kurve lässt sich zwar nicht so einfach wie bei bekannten geometrischen Figuren bestimmen, kann jedoch näherungsweise mit Ober- und Untersumme ermittelt werden.
Man unterteilt die Fläche in eine Reihe von Rechtecken bzw. Streifen, wobei sich zwei Möglichkeiten anbieten:
- Untersumme: Jeder Streifen wird so gesetzt, dass die linke Ecke genau den Funktionsgraphen berührt. Der Flächeninhalt aller Streifen zusammen ist dadurch kleiner als die gesuchte Fläche.
- Obersumme: Jeder Streifen wird so gesetzt, dass die rechte Ecke genau den Funktionsgraphen berührt. Der Flächeninhalt aller Streifen zusammen ist dadurch größer als die gesuchte Fläche.
Je mehr Streifen gewählt werden, desto kleiner ist der nicht erfasste Abstand bei der Untersumme bzw. desto kleiner ist die Überlappung bei der Obersumme. Das Ergebnis wird also immer genauer.
Die Idee: Bei unendlich vielen Streifen sollte man den exakten Flächeninhalt bekommen. Da sich "unendlich" nicht einfach einsetzen lässt, berechnet man den Flächeninhalt für $n$ Streifen. $n$ ist eine Variable, sodass man mit dem Limes das Verhalten für $n$ im Unendlichen erhält.
- Flächeninhalt der Untersumme $U$ für eine unbekannte Anzahl $n$ bestimmen
- Flächeninhalt der Obersumme $O$ für eine unbekannte Anzahl $n$ bestimmen
- Grenzwerte von $U$ und $O$ für $n\to\infty$ berechnen