Ober- und Untersumme

Die Integralrechnung wird zur Berechnung der Fläche in einem Intervall zwischen dem Graphen einer Funktion und der x-Achse genutzt.

$Fläche unter einem Funktionsgraphen$

Info

Bereits 260 v. Chr. entwickelte Archimedes die Streifenmethode, welche den Ursprung der Integralrechnung bildet.

Wenn man den Flächeninhalt nun ermitteln will, unterteilt man die Fläche in vertikale Streifen. Dabei ergeben sich zwei Möglichkeiten:

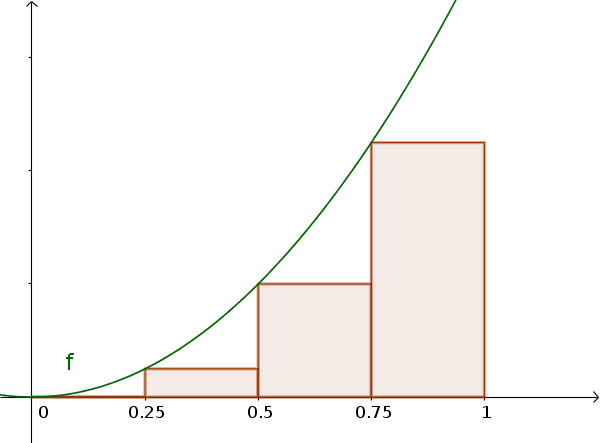
$Untersumme kleiner als gesuchter Flächeninhalt$

Die erste Einteilung der Fläche wird als Untersumme bezeichnet und ist kleiner als der Flächeninhalt.

$Obersumme größer als gesuchter Flächeninhalt$

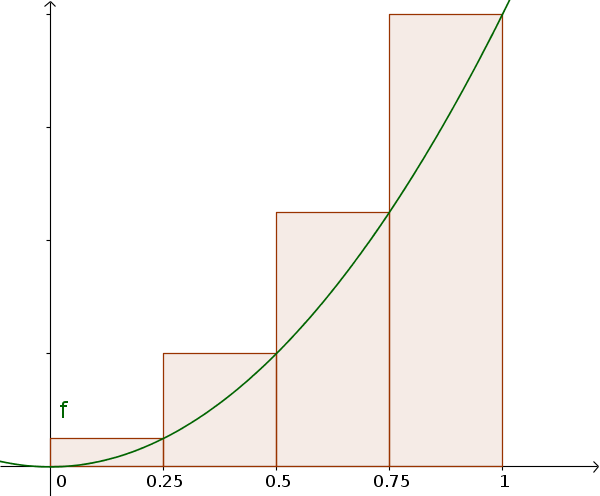
Hier handelt es sich um die Obersumme und die ist größer als der tatsächliche Flächeninhalt.

$\text{Untersumme} \le A \le \text{Obersumme}$

Merke

Je geringer man die Abstände zwischen den Streifen setzt (also je mehr Streifen), desto genauer wird das Ergebnis.

Beispiel

$f(x)=x^2$ im Intervall $[0; 1]$

Man kann nun die Flächeninhalte der Rechtecke (Breite ist $0,25$ und Höhe ist $x^2$) jeweils zusammenrechnen und erhält folgendes:

$U=0,25\cdot (0^2+0,25^2+0,5^2+0,75^2)$ $=\frac{7}{32}$
$O=0,25\cdot (0,25^2+0,5^2+0,75^2+1^2)$ $=\frac{15}{32}$
$\frac{7}{32} \le A \le \frac{15}{32}$

Bei höherer Streifenanzahl, wird das Ergebnis immer genauer. So hat man bei einer Streifenzahl von 256: $0,331\le A\le 0,335$

Obersumme / Untersumme, Integralrechnung, Fläche unter Kurve, Flächenberechnung, bestimmtes Integral

Kooperation mit dem Kanal von Mister Mathe

Der Flächeninhalt unterhalb einer Kurve lässt sich nicht so einfach bestimmen wie bei bekannten geometrischen Figuren. Ziel ist also diesen zuerst mit der bekannten Flächeninhaltsformel von Rechtecken näherungsweise zu bestimmen.

Dazu unterteilt man die Fläche in eine Reihe von Rechtecken bzw Streifen, wobei sich zwei Möglichkeiten anbieten:

Untersumme: Jeder Streifen wird so gesetzt, dass die linke Ecke genau den Funktionsgraphen berührt. Der Flächeninhalt aller Streifen zusammen ist dadurch kleiner als die gesuchte Fläche.
Obersumme: Jeder Streifen wird so gesetzt, dass die rechte Ecke genau den Funktionsgraphen berührt. Der Flächeninhalt aller Streifen zusammen ist dadurch größer als die gesuchte Fläche.

$\text{Untersumme} \le A \le \text{Obersumme}$

Je mehr Streifen gewählt werden, desto kleiner ist der nicht erfasste Abstand bei der Untersumme bzw. desto kleiner ist die Überlappung bei der Obersumme. Das Ergebnis wird immer genauer.

Diese Eigenschaft wird bei der Streifenmethode ausgenutzt, indem man den Grenzwert für unendlich Streifen bestimmt. Es handelt sich um die Herleitung des bestimmten Integrals.