Верхняя и нижняя сумма
Интегральное исчисление используется для того, чтобы вычислить площадь в интервале между графиком функции и осью X.
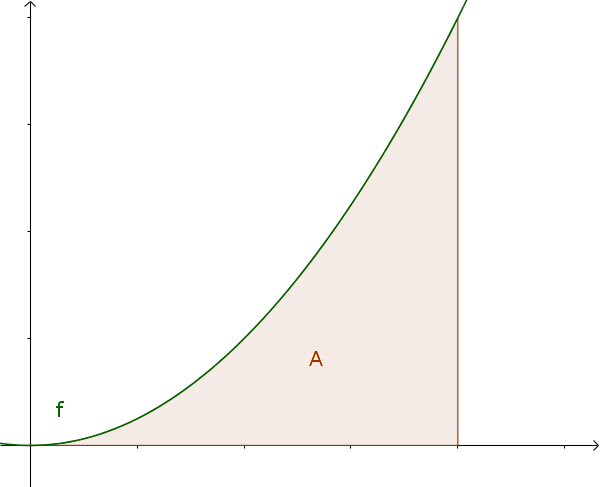
Информация
Если вы хотите вычислить площадь прямо сейчас, разбейте ее на вертикальные прямоугольники. Есть две возможности:
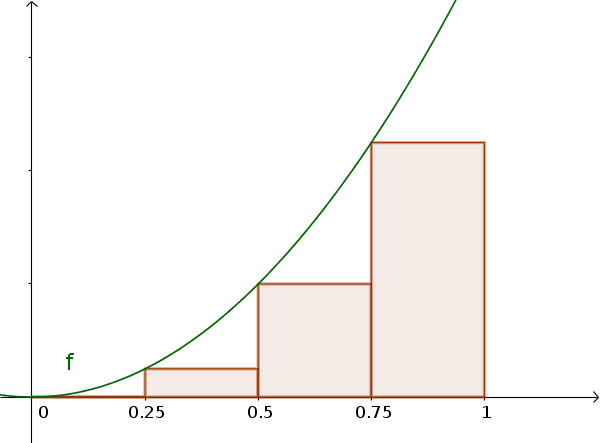
первое разбиение поверхности называется, нижней суммой и это меньше, чем площадь.
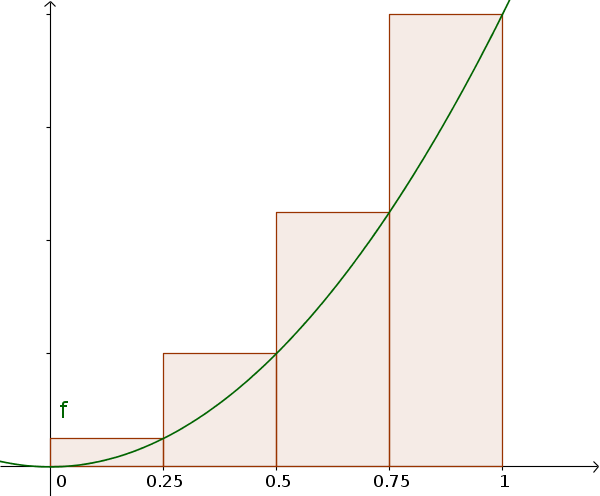
Это и есть верхняя сумма, которая больше, чем фактическая площадь .
$\text{нижняя сумма} \le A \le \text{верхняя сумма}$
Запомните
Например
$f(x)=x^2$ в интервале $[0; 1]$
Теперь вы можете рассчитать площади прямоугольников (ширина равна $0.25$ и высота, это $x^2$) и получаем следующее:
Нижняя сумма
$s=0.25\cdot (0^2+0.25^2+0.5^2+0.75^2)$ $=\frac{7}{32}$
Верхняя сумма
$S=0.25\cdot (0.25^2+0.5^2+0.75^2+1^2)$ $=\frac{15}{32}$
Результат
$\frac{7}{32} \le A \le \frac{15}{32}$
При большем количестве делений, результат становится все более точным. Итак, на ряде из 256 делений:
$0.331\le A\le 0.335$
