Upper and lower sum
Integral calculus is used to calculate the area in an interval between the graph of a function and the x-axis.
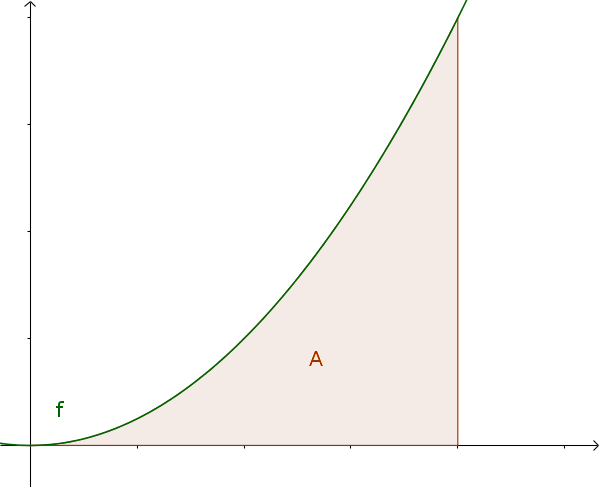
Info
If you want to determine the area now, one partitions the area into vertical rectangles. There are two possibilities:
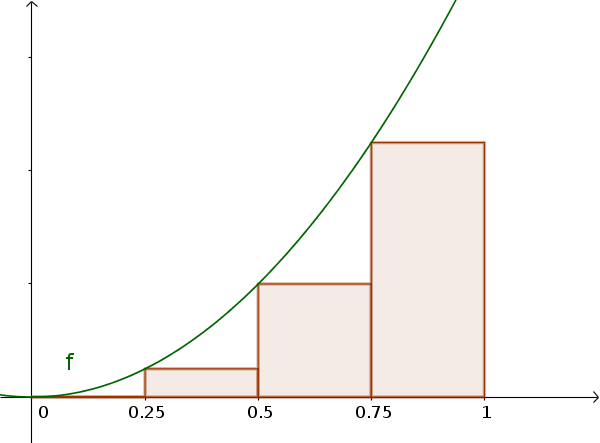
The first partition of the surface is called lower sum and is smaller than the area.
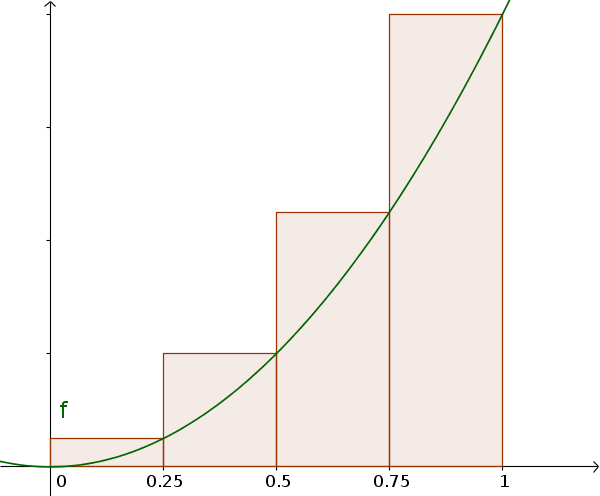
This is the upper sum which is larger than the actual area.
$\text{lower sum} \le A \le \text{upper sum}$
Remember
Example
$f(x)=x^2$ in the interval $[0; 1]$
You can now calculate the areas of the rectangles (width is $0.25$ and height is $x^2$) and get the following:
Lower sum
$s=0.25\cdot (0^2+0.25^2+0.5^2+0.75^2)$ $=\frac{7}{32}$
Upper sum
$S=0.25\cdot (0.25^2+0.5^2+0.75^2+1^2)$ $=\frac{15}{32}$
Result
$\frac{7}{32} \le A \le \frac{15}{32}$
With a higher number of partitions, the result becomes more and more accurate. So at a number of 256 partitions:
$0.331\le A\le 0.335$
