Partition of an interval

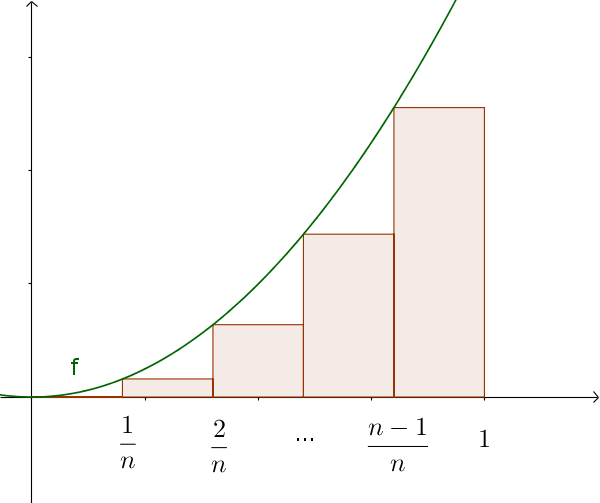
If you now let the number of partitions $n$ go against infinity, you will get the surface you are looking for. For this one forms the limit of the upper and lower sums for $n\to\infty$.

Example

$f(x)=x^2$ in the interval $[0; 1]$

1. Calculate lower sum

   The width is $\frac1n$ and the height is $x^2$.
   $s=\frac1n\cdot(0^2+(\frac1n)^2+(\frac2n)^2+...$ $+(\frac{n-1}{n})^2)$
   
   Remove brackets by squaring the numerator and denominator.
   $s=\frac1n\cdot(0^2+\frac{1^2}{n^2}+\frac{2^2}{n^2}+...$ $+\frac{(n-1)^2}{n^2})$
   
   Each denominator contains $n^2$, so you can expand brackets
   $s=\frac{1}{n^3}\cdot(0^2+1^2+2^2+...+(n-1)^2)$
   
   There is a trick to rewrite the parenthesis: All squares up to $m$ ($1^2+2^2+...+m^2$) make up:
   $\frac16\cdot\color{red}{m}\cdot(\color{red}{m}+1)\cdot(2\color{red}{m}+1)$
   Applied to our example, this means:
   $\color{red}{m}=\color{red}{(n-1)}$
   $s=\frac{1}{n^3}\cdot\frac16\cdot\color{red}{(n-1)}\cdot$ $(\color{red}{n-1}+1)\cdot(2\color{red}{(n-1)}+1)$
   $s=\frac16\cdot\frac{1}{n^3}\cdot(n-1)\cdot n\cdot(2n-1)$

2. Calculate upper sum

   The same again for the upper sum.
   $S=\frac1n\cdot((\frac1n)^2+(\frac2n)^2+...$ $+(\frac{n-1}{n})^2+1^2)$
   $S=\frac{1}{n^3}\cdot(1^2+2^2+...$ $+(n-1)^2+n^2)$
   $S=\frac16\cdot\frac{1}{n^3}\cdot n\cdot (n+1)\cdot(2n+1)$

3. Find limit

   Now the limit must be found.
   $s=\frac16\cdot\frac{1}{n^3}\cdot(n-1)\cdot n\cdot(2n-1)$ $=\frac16\cdot\frac{n-1}{n}\cdot \frac{n}{n}\cdot \frac{2n-1}{n}$
   
   $\lim\limits_{n \to \infty}{s}=$ $\lim\limits_{n \to \infty}{(\frac16\cdot\frac{n-1}{n}\cdot \frac{n}{n}\cdot \frac{2n-1}{n})}$ $=\frac16\cdot1\cdot1\cdot2=\frac13$
   
   $S=\frac16\cdot\frac{1}{n^3}\cdot n\cdot (n+1)\cdot(2n+1)$ $=\frac16\cdot\frac{n}{n}\cdot\frac{n+1}{n}\cdot\frac{2n+1}{n}$
   
   $\lim\limits_{n \to \infty}{S}=$ $\lim\limits_{n \to \infty}{(\frac16\cdot\frac{n}{n}\cdot\frac{n+1}{n}\cdot\frac{2n+1}{n})}$ $=\frac16\cdot1\cdot1\cdot2=\frac13$

4. Determine area

   For the area applies:
   $s \le A \le S$
   
   $\frac13 \le A \le \frac13$
   
   The area you are looking for is thus: $A=\frac13$