Математика ↠ Определенный интеграл ↠ Разбиение интервала

Разбиение интервала

!

Запомните

Чем больше делений вы устанавливаете с помощью, верхней или нижней суммы, тем точнее становится результат.

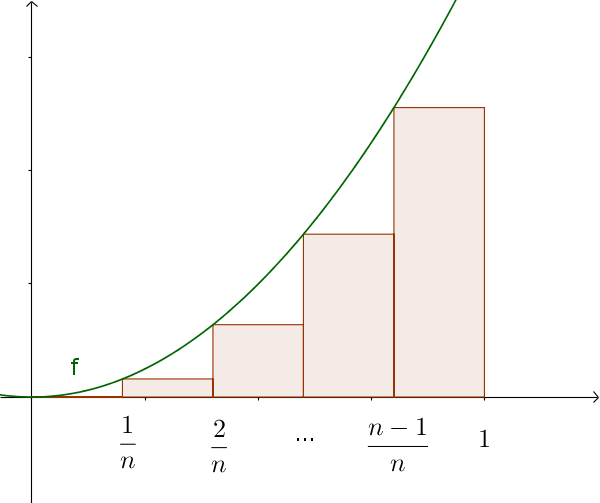
Если, вы позволите количество разделов $n$, идя против бесконечности, вы получите поверхность, которую ищете. Для этого образуется предел верхней и нижней сумм для $n\to\infty$.

i

Подсказка

Это просто вывод определенного интеграла.

Например

$f(x)=x^2$ в интервале $[0; 1]$

  1. Вычислите нижнюю сумму

    Ширина составляет $\frac1n$ и высота $x^2$.
    $s=\frac1n\cdot(0^2+(\frac1n)^2+(\frac2n)^2+...$ $+(\frac{n-1}{n})^2)$

    Раскройте скобки, возведя числитель и знаменатель в квадрат.
    $s=\frac1n\cdot(0^2+\frac{1^2}{n^2}+\frac{2^2}{n^2}+...$ $+\frac{(n-1)^2}{n^2})$

    Каждый знаменатель содержит $n^2$, так что вы можете раскрыть скобки
    $s=\frac{1}{n^3}\cdot(0^2+1^2+2^2+...+(n-1)^2)$

    Существует трюк, чтобы раскрыть скобки: все квадраты до $m$ ($1^2+2^2+...+m^2$) составить:
    $\frac16\cdot\color{red}{m}\cdot(\color{red}{m}+1)\cdot(2\color{red}{m}+1)$
    Применительно к нашему примеру это означает:
    $\color{red}{m}=\color{red}{(n-1)}$
    $s=\frac{1}{n^3}\cdot\frac16\cdot\color{red}{(n-1)}\cdot$ $(\color{red}{n-1}+1)\cdot(2\color{red}{(n-1)}+1)$
    $s=\frac16\cdot\frac{1}{n^3}\cdot(n-1)\cdot n\cdot(2n-1)$

  2. Вычислите верхнюю сумму

    То же самое и для верхней суммы.
    $S=\frac1n\cdot((\frac1n)^2+(\frac2n)^2+...$ $+(\frac{n-1}{n})^2+1^2)$
    $S=\frac{1}{n^3}\cdot(1^2+2^2+...$ $+(n-1)^2+n^2)$
    $S=\frac16\cdot\frac{1}{n^3}\cdot n\cdot (n+1)\cdot(2n+1)$

  3. Найдите предел

    Теперь этот предел должен быть найден.
    $s=\frac16\cdot\frac{1}{n^3}\cdot(n-1)\cdot n\cdot(2n-1)$ $=\frac16\cdot\frac{n-1}{n}\cdot \frac{n}{n}\cdot \frac{2n-1}{n}$

    $\lim\limits_{n \to \infty}{s}=$ $\lim\limits_{n \to \infty}{(\frac16\cdot\frac{n-1}{n}\cdot \frac{n}{n}\cdot \frac{2n-1}{n})}$ $=\frac16\cdot1\cdot1\cdot2=\frac13$

    $S=\frac16\cdot\frac{1}{n^3}\cdot n\cdot (n+1)\cdot(2n+1)$ $=\frac16\cdot\frac{n}{n}\cdot\frac{n+1}{n}\cdot\frac{2n+1}{n}$

    $\lim\limits_{n \to \infty}{S}=$ $\lim\limits_{n \to \infty}{(\frac16\cdot\frac{n}{n}\cdot\frac{n+1}{n}\cdot\frac{2n+1}{n})}$ $=\frac16\cdot1\cdot1\cdot2=\frac13$

  4. Найдите площадь

    Для площади применяется:
    $s \le A \le S$

    $\frac13 \le A \le \frac13$

    Таким образом, площадь, которую вы ищете, представляет: $A=\frac13$