Вычисление площадей под кривой
Площадь между кривой и осью x может быть вычислена с помощью определенного интеграла. Запомните следующее:
!
Запомни
При определенном интеграле числа, находящиеся выше оси х, являются положительными, а те, что ниже, - отрицательными.
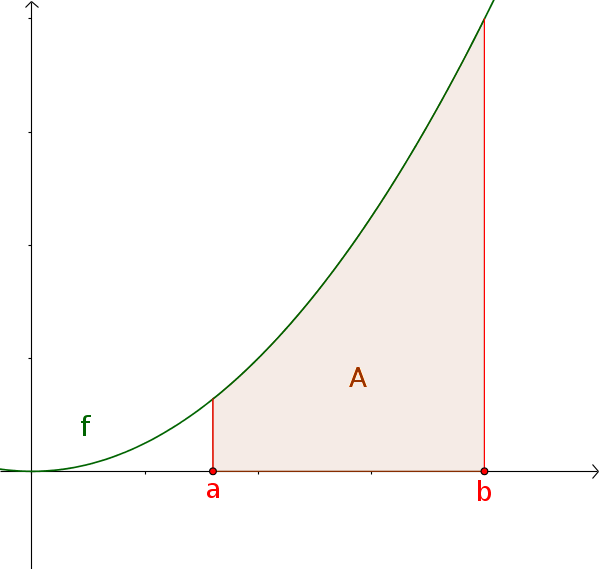
Определенный интеграл положительной функции
Площадь положительной функции $f(x)\ge0$ над $[a; b]$, соответствует определенному интегралу.
$A=\int_a^b f(x)\,\mathrm{d}x$
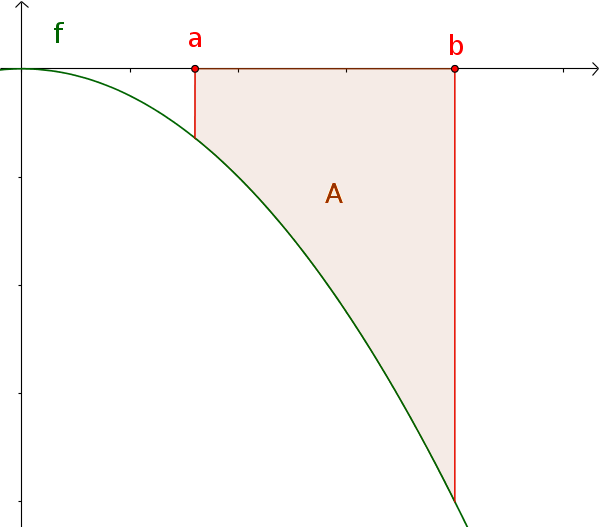
Определенный интеграл отрицательной функции
Площадь отрицательной функции $f(x)\le0$ над $[a; b]$, соответствует отрицательно определенному интегралу.
$A=-\int_a^b f(x)\,\mathrm{d}x$
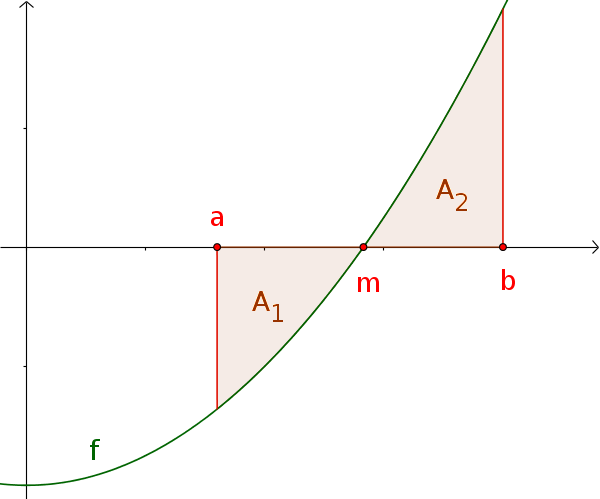
Определенные интегралы с изменением знака
При определенном интеграле функции, $f$ с изменением знака площади над $[a; b]$.
$A_2-A_1=\int_a^b f(x)\,\mathrm{d}x$
Площадью является:
$A=-\int_a^m f(x)\,\mathrm{d}x \,+$ $\int_m^b f(x)\,\mathrm{d}x$