Области между графиками
Отдельным случаем при вычислении площади между графиками функций является случай, когда площадь делится пересечением на несколько зон.
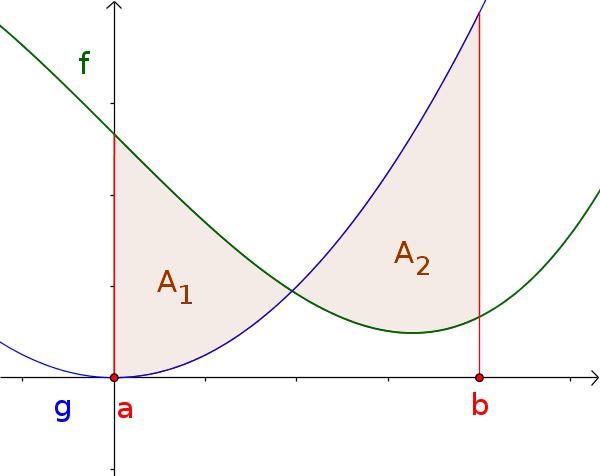
На рисунке: площадь $A_1$ находится ниже $f$ и выше $g$. Однако,площадь $A_2$, выше $f$ и ниже $g$.
В связи с этим, площади должны быть рассчитаны отдельно.
!
Запомни
Если одна из функций не является последовательно больше другой на протяжении всего интервала, необходимо вычислить области отдельно, а затем сложить их вместе.
Это происходит, когда координаты функций пересекаются в пределах интервала.
Это происходит, когда координаты функций пересекаются в пределах интервала.
i
Метод
- Определите точки пересечения и сформируйте интервалы
- Найдите разность функций
- Вычислите определенный интеграл для каждого интервала
- Определите площадь
Например
Определите область, заключенную в графике функций $f(x)=\frac16x^3-x$ и $g(x)=-\frac16x^3+\frac13x^2+x$.
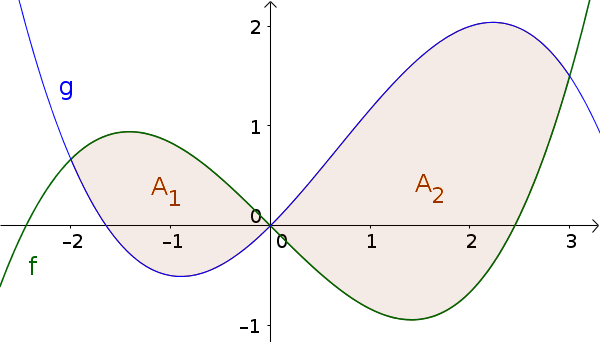
Подсказка: закрытая область - это область между внешними пересечениями.
-
Найдите точки пересечения
Установите равные функции для определения пересечений.
$f(x)=g(x)$
$\frac16x^3-x=-\frac16x^3+\frac13x^2+x$
$\frac13x^3-\frac13x^2-2x=0$
$x\cdot(\frac13x^2-\frac13x-2)=0$
$x_{S_1}=0$
$\frac13x^2-\frac13x-2=0\quad|\cdot3$
$x^2-x-6=0$
(Решите, квадратное уравнение, используя формулу квадратов I)
$x_{S_{2,3}}=\frac12\pm\sqrt{(\frac12)^2+6}$
$x_{S_2}=-2$ and $x_{S_3}=3$ -
Определите интервалы
$x_{S_1}=0$ находится между двумя точками пересечения и делит площадь на два участка, которые должны быть рассчитаны отдельно.
$x_{S_1}=0$, $x_{S_2}=-2$ and $x_{S_3}=3$
$A_1$ на $[-2;0]$
$A_2$ на $[0;3]$ -
Разность функций
Вычтем $g(x)$ от $f(x)$,объединим и определим первообразную .
$f(x)=\frac16x^3-x$
$g(x)=-\frac16x^3+\frac13x^2+x$
$h(x)=f(x)-g(x)$ $=(\frac16x^3-x)-$ $(-\frac16x^3+\frac13x^2+x)$ $=\frac13x^3-\frac13x^2-2x$
$H(x)=\frac{1}{12}x^4-\frac19x^3-x^2$ -
Найдите и вычислите определенные интегралы
Теперь для обоих интервалов необходимо определить интеграл.
$\int_a^b (f(x)-g(x))\,\mathrm{d}x$ $=\int_a^b h(x)\,\mathrm{d}x$ $= [H(x) + C]_a^b$ $= H(b) - H(a)$
$A_1$ на $[-2;0]$
$\int_{-2}^0 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x$ $=[\frac{1}{12}x^4-\frac19x^3-x^2]_{-2}^0$ $=0-(\frac{1}{12}\cdot(-2)^4-\frac19\cdot(-2)^3-(-2)^2)$
$=0-(-\frac{16}{9})$ $=\frac{16}{9}$
$A_2$ на $[0;3]$
$\int_0^3 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x$ $=[\frac{1}{12}x^4-\frac19x^3-x^2]_0^3$ $=(\frac{1}{12}\cdot3^4-\frac19\cdot3^3-3^2)-0$
$=(-\frac{21}{4})-0$ $=-\frac{21}{4}$ -
Определите площадь
Теперь площадь каждой части должна быть найдена и затем суммирована.
$A_1$ $=\int_{-2}^0 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x$ $=\frac{16}{9}$
$A_2$ $=|\int_0^3 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x|$ $=|-\frac{21}{4}|$ $=\frac{21}{4}$
$A=A_1+A_2$ $=\frac{16}{9}+\frac{21}{4}\approx7.03$
