Вычисление площади между кривыми

Определенный интеграл также может быть использован для вычисления площади между двумя графиками.

Нам необходимо найти замкнутую область между двумя функциями в интервале $[a;b]$. Для этого вычитаем меньшую площадь из большей ($f(x) > g(x)$ в интервале $[a;b]$):

Теперь правило суммы мы можем применить в обратном порядке.
Для того, чтобы формула сработала, $f(x) < g(x)$ в интервале $[a;b]$, одна велечина должна быть абсолютной.

Например

Вычислите площадь между графиками функций $f(x)=\frac12x^2+1$ и $g(x)=-\frac12x^2+x$ на протяжении интервала $[0.5; 2]$

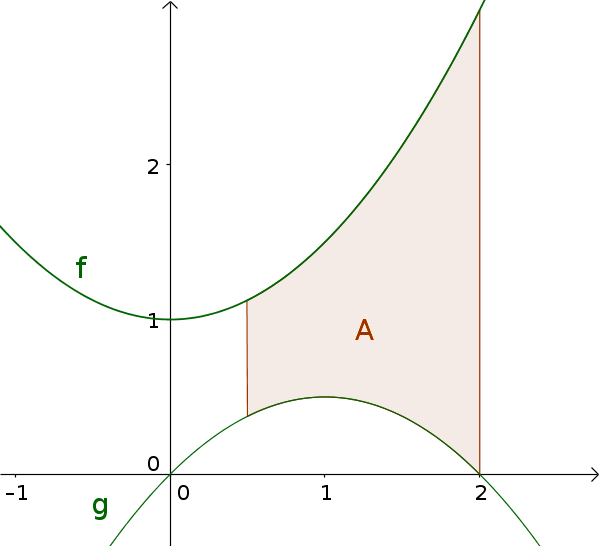
1. Дифференцируйте функции

   Сначала, $g(x)$ вычтите $f(x)$ и комбинируйте.
   $f(x)=\frac12x^2+1$
   $g(x)=-\frac12x^2+x$
   
   $h(x)=f(x)-g(x)$ $=(\frac12x^2+1)-$ $(-\frac12x^2+x)$ $=x^2-x+1$

2. Найдите определенный интеграл

   Вставьте пределы интегрирования и $h(x)$ в данный интеграл, вычислите интеграл.
   $\int_a^b (f(x)-g(x))\,\mathrm{d}x$ $=\int_a^b h(x)\,\mathrm{d}x$
   
   $\int_{0.5}^2 (x^2-x+1)\,\mathrm{d}x$

3. Вычислите интеграл

   $\int_a^b h(x) \, \mathrm{d}x$ $= [H(x) + C]_a^b$ $= H(b) - H(a)$
   
   $H(x)=\frac13x^3-\frac12x^2+x$
   
   $\int_{0.5}^2 (x^2-x+1)\,\mathrm{d}x$ $=[\frac13x^3-\frac12x^2+x]_{0.5}^2$ $=(\frac13\cdot2^3-\frac12\cdot2^2+2)-$ $(\frac13\cdot0.5^3-\frac12\cdot0.5^2+0.5)$
   $=\frac83-\frac{5}{12}$ $=\frac94$
   

4. Определите площадь

   $A=\int_{0.5}^2 (x^2-x+1)\,\mathrm{d}x$ $=\frac94$ $=2.25$