Расчет площади

Для функций без изменения знака в интервале $[a; b]$, площадь соответсвует сумме определенного интеграла:

$A=|\int_a^b f(x)\,\mathrm{d}x|$
i

Подсказка

Ранее уже говорилось о том, что область ниже оси х, имеет отрицательное значение для определенного интеграла.

Поскольку, отрицательной области нет, то при вычислении площадей под осью х необходимо изменить знак.

Например

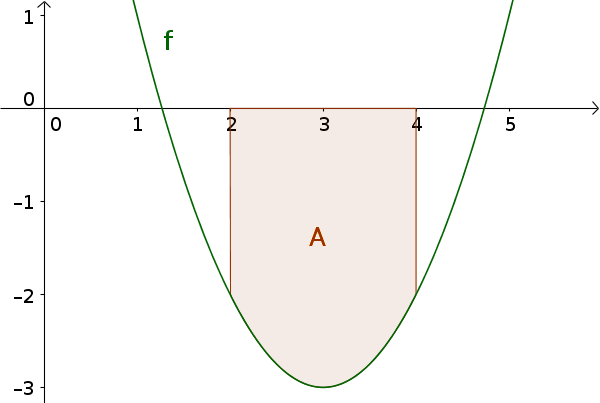
Найдите площадь между графиком функций $f(x)=x^2-6x+6$ и осью х через интервал $[2; 4]$

  1. Определенный интеграл

    Найдите определенный интеграл в соответствии с пределами интегрирования.
    $\int_2^4 (x^2-6x+6)\,\mathrm{d}x$

  2. Найдите интеграл

    Теперь вычислите интеграл. Для этого сначала найдите неопределенный интеграл.
    $\int_a^b f(x) \, \mathrm{d}x$ $= [F(x) + C]_a^b$ $= F(b) - F(a)$

    $F(x)=\frac13x^3-3x^2+6x$

    $\int_2^4 (x^2-6x+6)\,\mathrm{d}x$ $=[\frac13x^3-3x^2+6x]_2^4$ $=(\frac13\cdot4^3-3\cdot4^2+6\cdot4)-$ $(\frac13\cdot2^3-3\cdot2^2+6\cdot2)$
    $=-\frac83-\frac83$ $=-\frac{16}3$

  3. Определите площадь

    Схема графика говорит о том, что функция отрицательна в интервале $[2; 4]$. Поэтому знак нужно изменить.
    $A=|\int_2^4 f(x)\,\mathrm{d}x|$ $=|-\frac{16}3|$ $=\frac{16}3$ $\approx5.33$