Mathe ↠ Flächenberechnung mit Integralen ↠ Flächenberechnung

Flächenberechnung

Bei Funktionen ohne Vorzeichenwechsel im Intervall $[a; b]$ entspricht der Flächeninhalt dem Betrag des bestimmten Integrals:

$A=|\int_a^b f(x)\,\mathrm{d}x|$
i

Tipp

Hier wurde bereits beschrieben, dass die Fläche unterhalb der x-Achse beim bestimmten Integral negativ eingeht.

Da es keinen negativen Flächeninhalt gibt, muss man bei der Berechnung von Flächen unter der x-Achse noch das Vorzeichen wechseln.

Beispiel

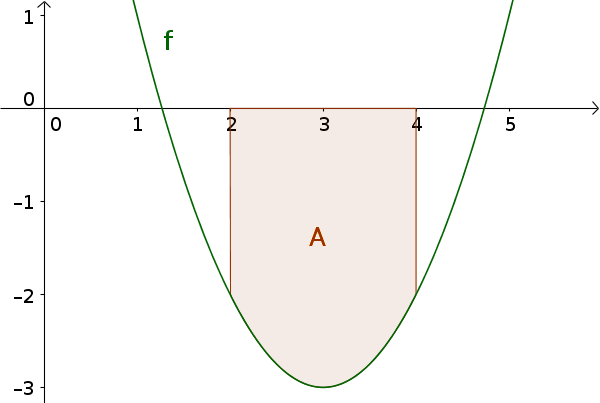
Berechne den Flächeninhalt zwischen dem Graphen der Funktion $f(x)=x^2-6x+6$ und der x-Achse über dem Intervall $[2; 4]$

Negative Fläche ohne Vorzeichenwechsel

  1. Bestimmtes Integral

    Das bestimmte Integral mit den gegeben Integrationsgrenzen aufstellen
    $\int_2^4 (x^2-6x+6)\,\mathrm{d}x$

  2. Integral berechnen

    Jetzt das Integral berechnen. Dazu vorher Stammfunktion bilden.
    $\int_a^b f(x) \, \mathrm{d}x$ $= [F(x) + C]_a^b$ $= F(b) - F(a)$

    $F(x)=\frac13x^3-3x^2+6x$

    $\int_2^4 (x^2-6x+6)\,\mathrm{d}x$ $=[\frac13x^3-3x^2+6x]_2^4$ $=(\frac13\cdot4^3-3\cdot4^2+6\cdot4)-$ $(\frac13\cdot2^3-3\cdot2^2+6\cdot2)$
    $=-\frac83-\frac83$ $=-\frac{16}3$

  3. Flächeninhalt bestimmen

    Die Skizze des Graphen zeigt, dass die Funktion im Intervall $[2; 4]$ negativ ist. Daher muss das Vorzeichen noch gewechselt werden
    $A=|\int_2^4 f(x)\,\mathrm{d}x|$ $=|-\frac{16}3|$ $=\frac{16}3$ $\approx5,33$

Flächenberechnung: Fläche ohne Vorzeichenwesel (VZW), Integralrechnung, bestimmtes Integral

Kooperation mit dem Kanal von Mister Mathe

Mit dem Abspielen dieses Videos akzeptierst du YouTubes Datenschutzerklärung.

Videos von YouTube immer laden

Beim bestimmten Integral gehen die Flächenstücke, welche oberhalb der x-Achse liegen, positiv und, die unterhalb, negativ ein.

Wenn die Funktion keine Nullstellen im gegebenen Intervall aufweist, lässt sich der Flächeinhalt $A$ im Bereich von $a$ bis $b$ ohne weitere Intervallaufteilung mit dem Betrag bestimmen:

$A=\left|\int_a^b f(x)\,\mathrm{d}x\right|$
  1. Überprüfe, dass sich keine Nullstellen von $f$ im Intervall $[a;b]$ befinden
  2. Bestimme die Stammfunktion $F$
  3. Nutze die Stammfunktion und den Hauptsatz der Differenzial- und Integralrechnung, um das bestimmte Integral auszurechnen: $\int_a^b f(x)\,\mathrm{d}x=F(b)-F(a)$
  4. Beachte, dass der Flächeninhalt nur positiv sein kann