Mathe ↠ Flächenberechnung mit Integralen

Flächenberechnung mit Integralen

Eine wichtige Anwendung der Integralrechnung ist das Berechnen der Fläche zwischen einem Funktionsgraphen und der x-Achse. Gesucht ist häufig eine Teil-Fläche von $x_1$ bis hin zu $x_2$. Man sagt dazu auch der Flächeninhalt unter der Funktion $f$ über dem Intervall $[x_1;x_2]$

Bestimmte Integrale

Rechnerisch erfolgt die Bestimmung des Flächeninhaltes mit dem bestimmten Integral. Dieses gibt die gerichtete Fläche unterhalb eines Funktionsgraphen innerhalb der Integrationsgrenzen $[a;b]$ an.

$\int_a^b f(x) \, \mathrm{d}x$

Der Hauptsatz der Differenzial- und Integralrechnung ermöglicht die Berechnung des Ausdrucks mit Hilfe der Stammfunktion $F$ und liefert einem eine konkrete Zahl. Die Stammfunktion sollte dazu vorher mit den Integraionsregeln ermittelt werden.

$\int_a^b f(x) \, \mathrm{d}x = F(b) - F(a)$
!

Merke

Beim bestimmten Integral gehen die Flächenstücke, welche oberhalb der x-Achse liegen, positiv und, die unterhalb, negativ ein.

Zur Flächenberechnung sollte man wissen, wo der Funktionsgraph seine Nullstellen hat. Nun wird differenziert, ob die Nullstellen im Intervall liegen (dann Intervallaufteilung) oder nicht (Flächenberechnung ohne VZW).

Flächenberechnung ohne Vorzeichenwechsel

Bei Funktionen ohne Vorzeichenwechsel (also ohne Nullstellen) im Intervall $[a; b]$ entspricht der Flächeninhalt dem Betrag des bestimmten Integrals:

$A=\left|\int_a^b f(x)\,\mathrm{d}x\right|$

Beispiel

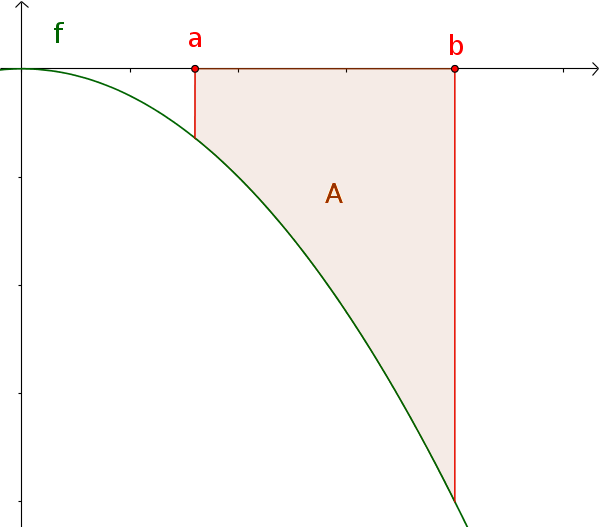
Negative Fläche ohne Vorzeichenwechsel

Da die Fläche in diesem Beispiel unterhalb der x-Achse liegt, ist das Ergebnis des bestimmten Integrals negativ und muss daher mit -1 multipliziert werden: $A=-\int_a^b f(x)\,\mathrm{d}x$

Flächenberechnung durch Intervallaufteilung

Wenn der Funktionsgraph im Intervall mindestens eine Nullstelle (und somit einen Vorzeichenwechsel) besitzt, liegt die Fläche teilweise über und teilweise unterhalb der x-Achse. Wir trennen dazu das Intervall an den einzelnen Nullstellen und berechnen jeweils das bestimmte Integral für die einzelnen Flächenstücke. Deren Beträge (also der positive Wert) werden anschließend addiert.

Beispiel

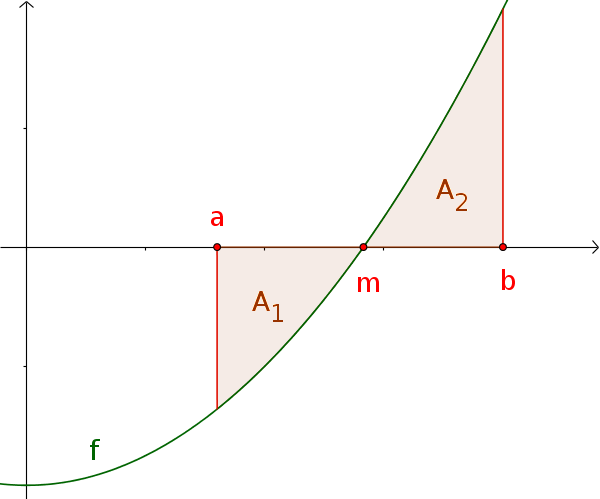
Fläche mit Vorzeichenwechsel

Hier muss das Intervall aufgeteilt werden in $[a;m]$ und $[m;b]$. Der Flächeninhalt entspricht somit also: $A=|\int_a^m f(x)\,\mathrm{d}x| \,+$ $|\int_m^b f(x)\,\mathrm{d}x|$

Fläche zwischen Funktionsgraphen

Wenn die Fläche zwischen zwei Funktionsgraphen liegt, sind die Schnittstellen (statt Nullstellen) dafür entscheidend, ob man eine Intervallaufteilung durchführen muss.

Fläche ohne Schnittpunkt

eingeschlossene Fläche zwischen zwei Funktionsgraphen

Für die Fläche ohne Schnittpunkte dazwischen gilt:

$A=|\int_a^b (f(x)-g(x))\,\mathrm{d}x|$

Fläche getrennt durch Schnittpunkt

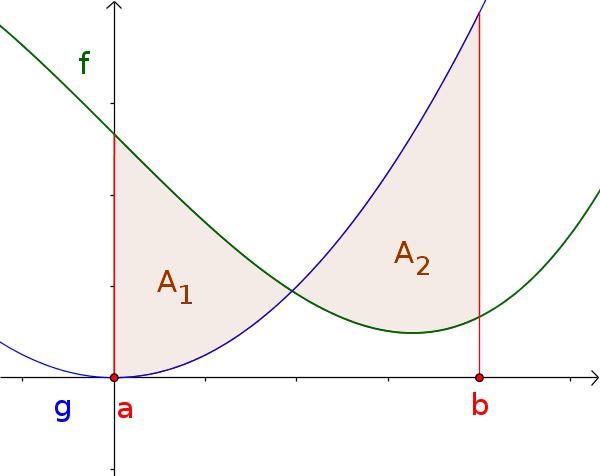
Ansonsten müssen bei einem Schnittpunkt im Intervall die daraus entstandenen Teilflächen einzeln berechnet und addiert werden: $A=A_1+A_2$

eingeschlossene Teilflächen zwischen zwei Funktionsgraphen mit Schnittpunkt
Quiz über Flächenberechnung mit Integralen starten