Flächenberechnung durch Intervallaufteilung
Eine Ausnahme bei der Flächenberechnung bilden Funktionen mit Vorzeichenwechsel im Intervall $[a; b]$. Das bedeutet, die Fläche liegt teilweise über und teilweise unterhalb der x-Achse.
!
Merke
Falls die gesuchte Fläche sowohl ober- als auch unterhalb der x-Achse liegt, muss man die Teilflächen einzeln berechnen.
Das tritt ein, wenn die Funktion im Intervall eine Nullstelle besitzt.
Das tritt ein, wenn die Funktion im Intervall eine Nullstelle besitzt.
i
Vorgehensweise
- Nullstellen ermitteln und Intervalle bilden
- Bestimmte Integrale für die einzelnen Intervalle berechnen
- Flächeninhalt bestimmen
Beispiel
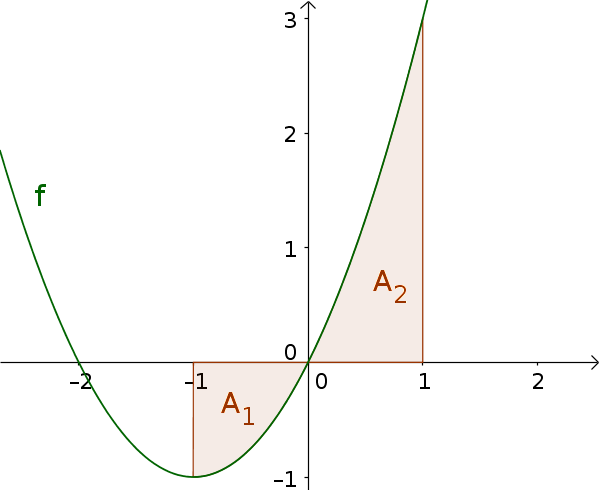
Berechne den Flächeninhalt zwischen dem Graphen der Funktion $f(x)=x^2+2x$ und der x-Achse über dem Intervall $[-1; 1]$
-
Intervalle bilden
Zuerst berechnet man die Nullstelle(n) der Funktion.
$x^2+2x=0$
(Quadratische Gleichung lösen, z.B. Ausklammern)
$x(x+2)=0$
$x_{N_1}=0$ und $x_{N_2}=-2$
$x_{N_1}=0$ liegt im Intervall $[-1; 1]$. Daher muss die Fläche in zwei Teilstücke unterteilt werden:
$A_1$ über $[-1;0]$
$A_2$ über $[0;1]$ -
Bestimmte Integrale aufstellen und berechnen
Für beide Intervalle muss nun jeweils ein Integral aufgestellt und berechnet werden.
$\int_a^b f(x) \, \mathrm{d}x$ $= [F(x) + C]_a^b$ $= F(b) - F(a)$
$F(x)=\frac13x^3+x^2$
$A_1$ über $[-1;0]$:
$\int_{-1}^0 (x^2+2x) \, \mathrm{d}x$ $= [\frac13x^3+x^2]_{-1}^0$ $= \frac13\cdot0^3+0^2 -$ $\frac13\cdot(-1)^3+(-1)^2$
$=0-\frac23$ $=-\frac23$
$A_2$ über $[0;1]$:
$\int_0^1 (x^2+2x) \, \mathrm{d}x$ $= [\frac13x^3+x^2]_0^1$ $= \frac13\cdot1^3+1^2 -$ $\frac13\cdot0^3+0^2$
$=\frac43-0$ $=\frac43$ -
Flächeninhalt bestimmen
Jetzt müssen die Inhalte der Flächenstücke bestimmt und dann addiert werden.
$A_1=|\int_{-1}^0 f(x)\,\mathrm{d}x|$ $=|-\frac23|$ $=\frac23$
$A_2=\int_0^1 f(x)\,\mathrm{d}x$ $=\frac43$
$A=A_1+A_2$ $=\frac23+\frac43=2$
Flächenberechnung: Fläche mit Vorzeichenwesel (VZW), Integralrechnung, bestimmtes Integral
Kooperation mit dem Kanal von Mister Mathe

