Flächeninhalt unter Funktionsgraph
Der Flächeninhalt zwischen einem Graphen und der x-Achse lässt sich mit dem bestimmten Integral berechnen. Dabei solltest du folgendes beachten:
!
Merke
Beim bestimmten Integral gehen die Flächenstücke, welche oberhalb der x-Achse liegen, positiv und, die unterhalb, negativ ein.
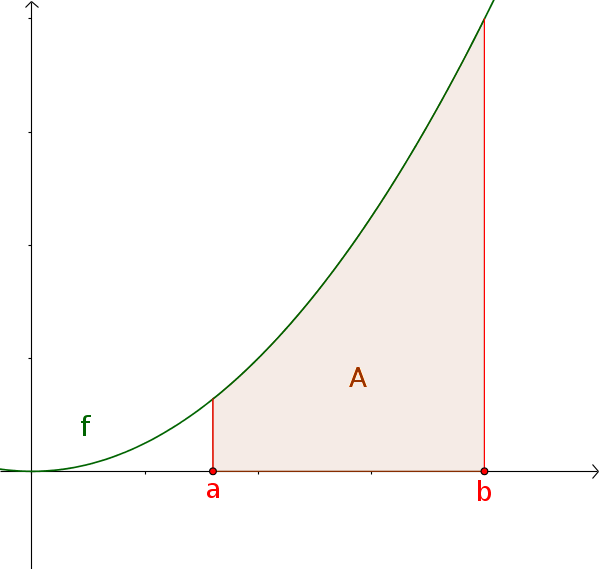
Bestimmtes Integral einer positiven Funktion
Der Flächeninhalt unter einer positiven Funktion $f(x)\ge0$ über $[a; b]$ entspricht dem bestimmten Integral.
$A=\int_a^b f(x)\,\mathrm{d}x$
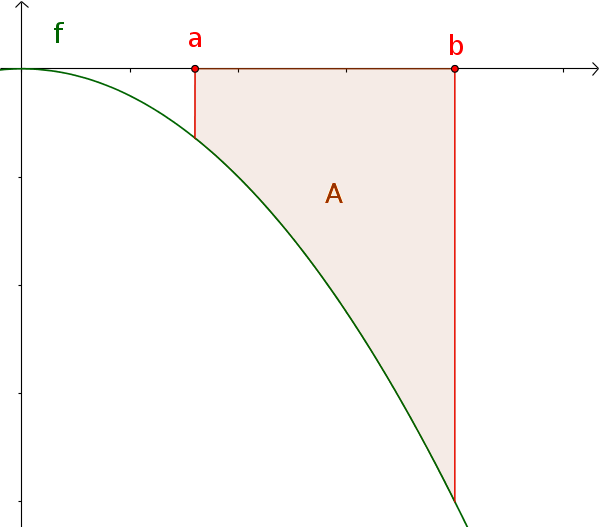
Bestimmtes Integral einer negativen Funktion
Der Flächeninhalt unter einer negativen Funktion $f(x)\le0$ über $[a; b]$ entspricht dem negativen bestimmten Integral.
$A=-\int_a^b f(x)\,\mathrm{d}x$
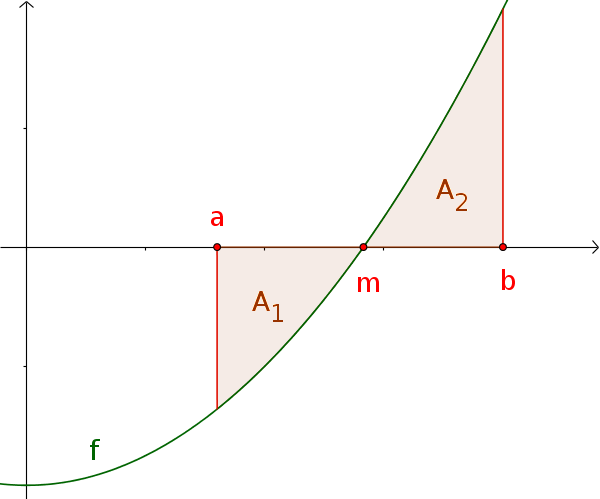
Bestimmtes Integral einer Funktion mit Vorzeichenwechsel
Das bestimmte Integral einer Funktion $f$ mit Vorzeichenwechsel entspricht der Flächenbilanz über $[a; b]$.
$A_2-A_1=\int_a^b f(x)\,\mathrm{d}x$
Der Flächeninhalt ist also:
$A=-\int_a^m f(x)\,\mathrm{d}x \,+$ $\int_m^b f(x)\,\mathrm{d}x$
Fläche unter Graph, Integralrechnung, Flächenberechnung, bestimmtes Intergral
Kooperation mit dem Kanal von Mister Mathe
Ein Vorzeichenwechsel tritt genau dann ein, wenn die Funktion innerhalb des gesuchten Intervalls eine Nullstelle hat. Zum Berechnen der Fläche unterhalb eines Funktionsgraphen in einem Intervall $[a;b]$, geht man also folgendermaßen vor:
- Nullstelle(n) der Funktion bestimmen
- Falls Nullstelle $x_N$ im Intervall liegt: Intervall aufteilen in $[a;x_N]$ und $[x_N;b]$
- Den Betrag der Flächenstücke einzeln mit dem bestimmten Integral berechnen. Wichtig: Negative Vorzeichen entfernen!

