Area under a curve
The area between a curve and the x-axis can be calculated with the definite integral. You should note the following:
!
Remember
For the definite integral, the partitions above the x-axis are positive and those below, negative.
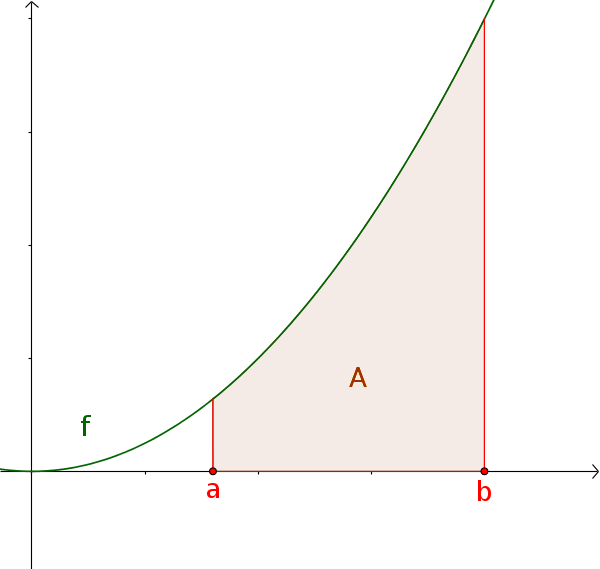
Definite integral of a positive function
The area under a positive function $f(x)\ge0$ over $[a; b]$ corresponds to the definite integral.
$A=\int_a^b f(x)\,\mathrm{d}x$
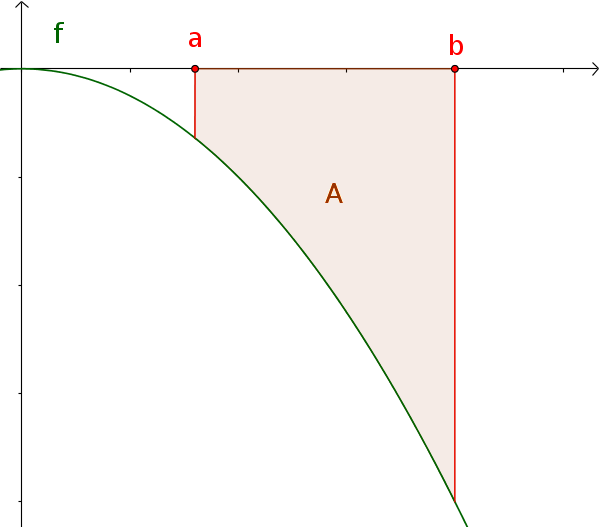
Definite integral of a negative function
The area under a negative function $f(x)\le0$ over $[a; b]$ corresponds to the negative definite integral.
$A=-\int_a^b f(x)\,\mathrm{d}x$
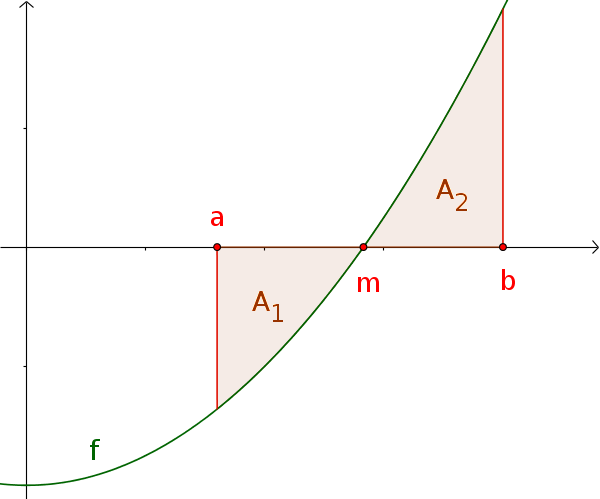
Definite integral of a function with sign change
The definite integral of a function $f$ with sign change corresponds to the signed area over $[a; b]$.
$A_2-A_1=\int_a^b f(x)\,\mathrm{d}x$
Therefore the area is:
$A=-\int_a^m f(x)\,\mathrm{d}x \,+$ $\int_m^b f(x)\,\mathrm{d}x$