Math ↠ Calculating areas with integrals ↠ Calculating the area

Calculating the area

For functions without change of sign in the interval $[a; b]$, the area corresponds to the amount of the definite integral:

$A=|\int_a^b f(x)\,\mathrm{d}x|$
i

Hint

Here it has already been described that the area below the x-axis is negative for the definite integral.

Since there is no negative area, one must change the sign when calculating areas under the x-axis.

Example

Find the area between the graph of the function $f(x)=x^2-6x+6$ and the x-axis over the interval $[2; 4]$

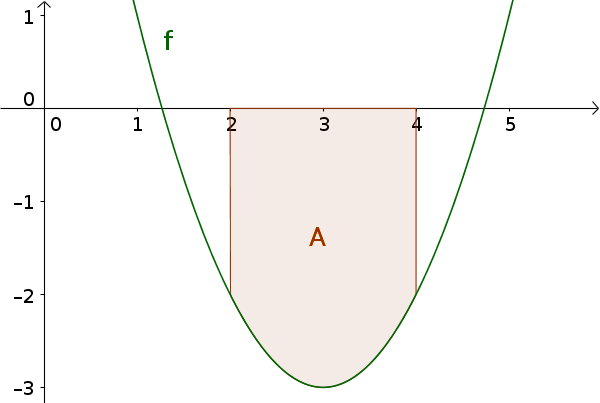
  1. Definite integral

    Set up the definite integral with the given limits of integration
    $\int_2^4 (x^2-6x+6)\,\mathrm{d}x$

  2. Find the integral

    Now calculate the integral. To do this calculate antiderivative first.
    $\int_a^b f(x) \, \mathrm{d}x$ $= [F(x) + C]_a^b$ $= F(b) - F(a)$

    $F(x)=\frac13x^3-3x^2+6x$

    $\int_2^4 (x^2-6x+6)\,\mathrm{d}x$ $=[\frac13x^3-3x^2+6x]_2^4$ $=(\frac13\cdot4^3-3\cdot4^2+6\cdot4)-$ $(\frac13\cdot2^3-3\cdot2^2+6\cdot2)$
    $=-\frac83-\frac83$ $=-\frac{16}3$

  3. Determine area

    The sketch of the graph shows that the function is negative in the interval $[2; 4]$. Therefore, the sign has to be changed
    $A=|\int_2^4 f(x)\,\mathrm{d}x|$ $=|-\frac{16}3|$ $=\frac{16}3$ $\approx5.33$