Нахождение площади путем разбиения

Исключением из правил служит расчет площадей функций с изменением знака в интервале $[a; b]$. Это означает, что область находится частично выше и частично ниже оси X.

Например

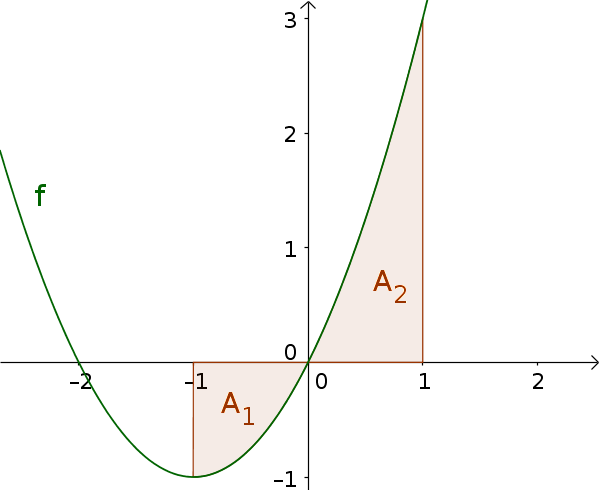
Рассчитайте площадь между графиком функций $f(x)=x^2+2x$ и осью х в интервале $[-1; 1]$

1. Найдите интервалы

   Сначала вычислите нули функции.
   $x^2+2x=0$
   (Решите квадратное уравнение, раскрыв скобки)
   $x(x+2)=0$
   $x_{N_1}=0$ и $x_{N_2}=-2$
   
   $x_{N_1}=0$ находится в интервале $[-1; 1]$. Поэтому площадь нужно разделить на две части:
   $A_1$ на $[-1;0]$
   $A_2$ на $[0;1]$
   

2. Найдите и вычислите определенные интегралы

   Теперь для обоих интервалов необходимо вычислить интеграл.
   $\int_a^b f(x) \, \mathrm{d}x$ $= [F(x) + C]_a^b$ $= F(b) - F(a)$
   $F(x)=\frac13x^3+x^2$
   
   $A_1$ на $[-1;0]$:
   $\int_{-1}^0 (x^2+2x) \, \mathrm{d}x$ $= [\frac13x^3+x^2]_{-1}^0$ $= \frac13\cdot0^3+0^2 -$ $\frac13\cdot(-1)^3+(-1)^2$
   $=0-\frac23$ $=-\frac23$
   
   
   $A_2$ на $[0;1]$:
   $\int_0^1 (x^2+2x) \, \mathrm{d}x$ $= [\frac13x^3+x^2]_0^1$ $= \frac13\cdot1^3+1^2 -$ $\frac13\cdot0^3+0^2$
   $=\frac43-0$ $=\frac43$
   

3. Определите площадь

   Теперь площадь каждой части раздела должна быть определена, а затем суммирована.
   $A_1=|\int_{-1}^0 f(x)\,\mathrm{d}x|$ $=|-\frac23|$ $=\frac23$
   $A_2=\int_0^1 f(x)\,\mathrm{d}x$ $=\frac43$
   
   $A=A_1+A_2$ $=\frac23+\frac43=2$