Teilflächen zwischen Funktionsgraphen
Ein Sonderfall bei der Berechnung der Fläche zwischen Funktionsgraphen ist, wenn die Fläche durch einen Schnittpunkt in mehrere Teilflächen zerfällt.
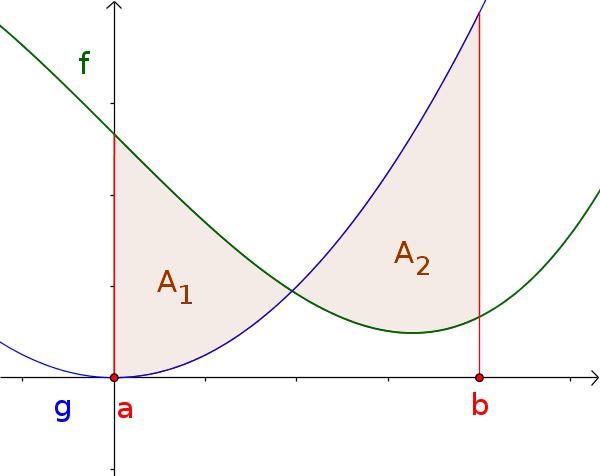
Zum Bild: Die Fläche $A_1$ liegt unterhalb von $f$ und oberhalb von $g$. Die Fläche $A_2$ hingegen liegt oberhalb von $f$ und unterhalb von $g$.
Aufgrund des Wechsels müssen die Flächen einzeln berechnet werden.
!
Merke
Falls eine Funktion im gesamten Intervall nicht durchweg größer ist als die andere, muss man die Teilflächen einzeln berechnen und dann addieren.
Das tritt ein, wenn die Funktionen innerhalb des Intervalls einen Schnittpunkt besitzen.
Das tritt ein, wenn die Funktionen innerhalb des Intervalls einen Schnittpunkt besitzen.
i
Vorgehensweise
- Schnittstellen ermitteln und Intervalle bilden
- Differenzenfunktion bilden
- Bestimmte Integrale für die einzelnen Intervalle berechnen
- Flächeninhalt bestimmen
Beispiel
Berechne die von den Graphen der Funktionen $f(x)=\frac16x^3-x$ und $g(x)=-\frac16x^3+\frac13x^2+x$ eingeschlossene Fläche.
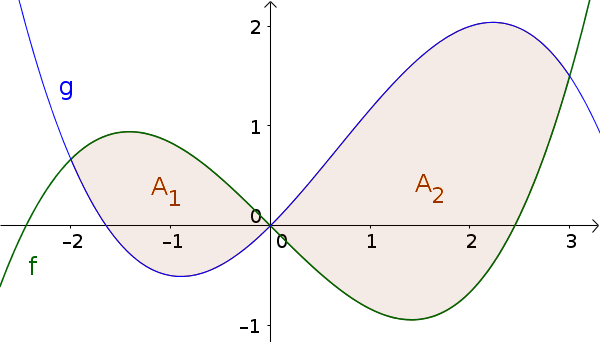
Tipp: Eingeschlossene Fläche bedeutet die Fläche zwischen den äußeren Schnittpunkten.
-
Schnittstellen berechnen
Funktionen gleichsetzen, um Schnittstellen zu berechnen.
$f(x)=g(x)$
$\frac16x^3-x=-\frac16x^3+\frac13x^2+x$
$\frac13x^3-\frac13x^2-2x=0$
$x\cdot(\frac13x^2-\frac13x-2)=0$
$x_{S_1}=0$
$\frac13x^2-\frac13x-2=0\quad|\cdot3$
$x^2-x-6=0$
(Quadratische Gleichung lösen, z.B. PQ-Formel)
$x_{S_{2,3}}=\frac12\pm\sqrt{(\frac12)^2+6}$
$x_{S_2}=-2$ und $x_{S_3}=3$ -
Intervalle bilden
$x_{S_1}=0$ liegt zwischen den beiden anderen Schnittpunkten und teilt die Fläche in zwei Teilstücke, welche einzeln berechnet werden müssen.
$x_{S_1}=0$, $x_{S_2}=-2$ und $x_{S_3}=3$
$A_1$ über $[-2;0]$
$A_2$ über $[0;3]$ -
Differenzenfunktion
$g(x)$ von $f(x)$ subtrahieren, zusammengefassen und Stammfunktion bilden.
$f(x)=\frac16x^3-x$
$g(x)=-\frac16x^3+\frac13x^2+x$
$h(x)=f(x)-g(x)$ $=(\frac16x^3-x)-$ $(-\frac16x^3+\frac13x^2+x)$ $=\frac13x^3-\frac13x^2-2x$
$H(x)=\frac{1}{12}x^4-\frac19x^3-x^2$ -
Bestimmte Integrale aufstellen und berechnen
Für beide Intervalle muss nun jeweils ein Integral aufgestellt und berechnet werden.
$\int_a^b (f(x)-g(x))\,\mathrm{d}x$ $=\int_a^b h(x)\,\mathrm{d}x$ $= [H(x) + C]_a^b$ $= H(b) - H(a)$
$A_1$ über $[-2;0]$
$\int_{-2}^0 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x$ $=[\frac{1}{12}x^4-\frac19x^3-x^2]_{-2}^0$ $=0-(\frac{1}{12}\cdot(-2)^4-\frac19\cdot(-2)^3-(-2)^2)$
$=0-(-\frac{16}{9})$ $=\frac{16}{9}$
$A_2$ über $[0;3]$
$\int_0^3 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x$ $=[\frac{1}{12}x^4-\frac19x^3-x^2]_0^3$ $=(\frac{1}{12}\cdot3^4-\frac19\cdot3^3-3^2)-0$
$=(-\frac{21}{4})-0$ $=-\frac{21}{4}$ -
Flächeninhalt bestimmen
Jetzt müssen die Inhalte der Flächenstücke bestimmt und dann addiert werden.
$A_1$ $=\int_{-2}^0 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x$ $=\frac{16}{9}$
$A_2$ $=|\int_0^3 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x|$ $=|-\frac{21}{4}|$ $=\frac{21}{4}$
$A=A_1+A_2$ $=\frac{16}{9}+\frac{21}{4}\approx7,03$
Fläche zwischen zwei Graphen die sich schneiden mit Integral berechnen, Fläche zwischen zwei Kurven
Kooperation mit dem Kanal von Mister Mathe

