Erklärung am Einheitskreis
Ein Kreis mit einem Radius von $r=1$, der um den Ursprung eines Koordinatensystems gezeichnet wurde, bezeichnet man als Einheitskreis.
Sinus und Kosinus kann man nun auf den Einheitskreis anwenden:
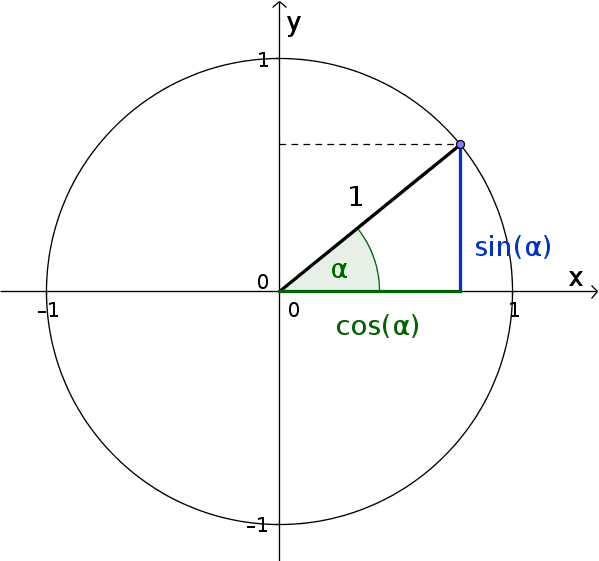
Da die Hypotenuse ($\text{HY}$) im Einheitskreis gleich dem Radius $1$ ist, gilt:
$\sin(\alpha)=\frac{\color{blue}{\text{GK}}}{\text{HY}}=\frac{\color{blue}{\text{GK}}}{1}$ $=\color{blue}{\text{Gegenkathete}}$
$\cos(\alpha)=\frac{\color{green}{\text{AK}}}{\text{HY}}=\frac{\color{green}{\text{AK}}}{1}$ $=\color{green}{\text{Ankathete}}$
$\cos(\alpha)=\frac{\color{green}{\text{AK}}}{\text{HY}}=\frac{\color{green}{\text{AK}}}{1}$ $=\color{green}{\text{Ankathete}}$
Man kann sich nun vorstellen, dass sich die Hypotenuse entgegen des Uhrzeigersinns dreht. Dabei ist die Länge der Ankathete bzw. Gegenkathete abhängig von der Größe des Winkels $\alpha$.
Um das nun als Funktion auszudrücken, ersetzt man $\alpha$ durch $x$ und die gesuchte Größe ($\text{Gegenkathete}$/$\text{Ankathete}$) durch $y$:
$y=\sin(x)$
$y=\cos(x)$
$y=\cos(x)$

