Explanation at the unit circle
A circle with a radius of $r=1$ drawn around the origin of a coordinate system is called a unit circle.
You can now apply sine and cosine to the unit circle:
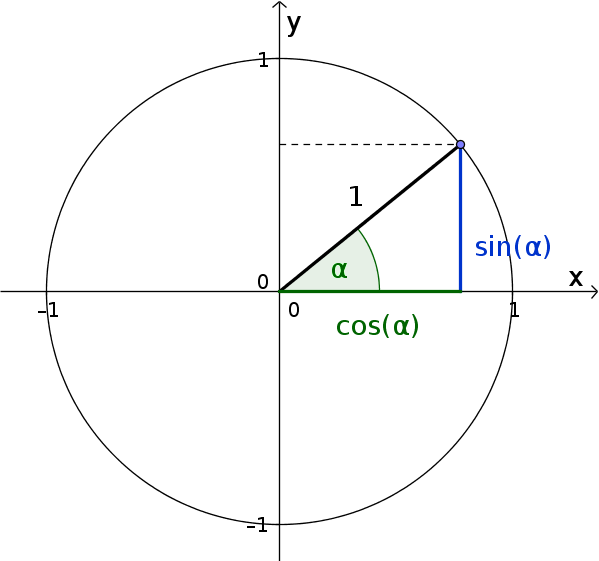
Since the hypotenuse ($\text{HY}$) in the unit circle is equal to the radius $1$, the following applies:
$\sin(\alpha)=\frac{\color{blue}{\text{O}}}{\text{HY}}=\frac{\color{blue}{\text{O}}}{1}$ $=\color{blue}{\text{opposite}}$
$\cos(\alpha)=\frac{\color{green}{\text{A}}}{\text{HY}}=\frac{\color{green}{\text{A}}}{1}$ $=\color{green}{\text{adjacent}}$
$\cos(\alpha)=\frac{\color{green}{\text{A}}}{\text{HY}}=\frac{\color{green}{\text{A}}}{1}$ $=\color{green}{\text{adjacent}}$
You can now imagine that the hypotenuse rotates counterclockwise. The length of the adjacent or opposite depends on the size of the angle $\alpha$.
To express this as a function, replace $\alpha$ with $x$ and the desired size ($\text{opposite}$/$\text{adjacent}$) with $y$:
$y=\sin(x)$
$y=\cos(x)$
$y=\cos(x)$

