Stretching and compressing

a) parallel to the y-axis:

The graphs of $y=\sin(x)$ and $y=\cos(x)$ are stretched and compressed with the factor $a$ parallel to the y-axis. This changes the amplitude. The general formula is:

$y=a\cdot\sin(x)$
$y=a\cdot\cos(x)$

Remember

If $|a|$ > 1, the graph is stretched.
If $|a|$ < 1, the graph is compressed.

If $a$ < 0, the graph is mirrored on the x-axis
The amplitude (maximum deflection) is $|a|$

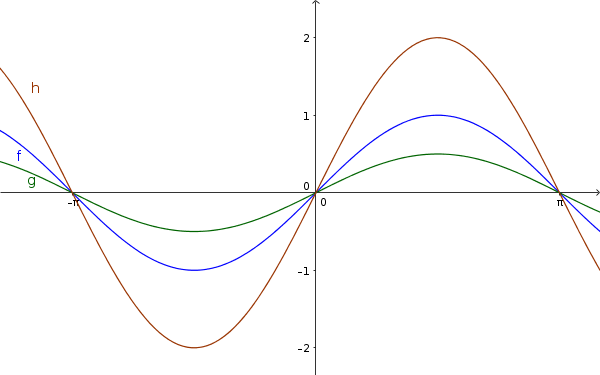
Example

$\color{green}{g(x)=\frac12\sin(x)}$
$\color{blue}{f(x)=\sin(x)}$
$\color{brown}{h(x)=2\sin(x)}$

b) parallel to the x-axis:

The graphs of $y=\sin(x)$ and $y=\cos(x)$ are stretched or compressed with the factor $b$ parallel to the x-axis. The period changes. The general formula is:

$y=\sin(b\cdot x)$
$y=\cos(b\cdot x)$

Remember

If $|b|$ > 1, the graph is compressed (the period is reduced).
If $|b|$ < 1, the graph is stretched (the period is increased).

If $b$ < 0, the graph is mirrored on the y-axis
The period (repetition) is $\frac{2\pi}{|b|}$

Beispiel

$\color{green}{g(x)=\sin(\frac12x)}$
$\color{blue}{f(x)=\sin(x)}$
$\color{brown}{h(x)=\sin(2x)}$