Растяжение и сжатие
a) параллельно оси y:
Графики $y=\sin(x)$ и $y=\cos(x)$ растягиваются и сжимаются с коэффициентом $a$ параллельно оси y. Это изменяет амплитуду. Общая формула такова:
$y=a\cdot\sin(x)$
$y=a\cdot\cos(x)$
$y=a\cdot\cos(x)$
!
Запомните
- Если $|a|$ > 1, график растянут.
- Если $|a|$ < 1, график сжат.
- Если $a$ < 0, график зеркальный на оси x
- Амплитуда (максимальное отклонение) равна $|a|$
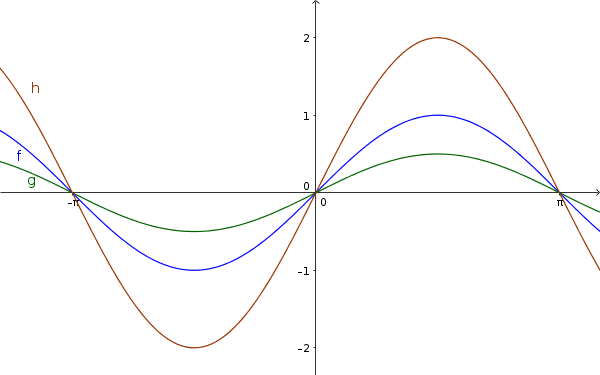
Например
$\color{green}{g(x)=\frac12\sin(x)}$
$\color{blue}{f(x)=\sin(x)}$
$\color{brown}{h(x)=2\sin(x)}$
b) параллельно оси x:
Графики $y=\sin(x)$ и $y=\cos(x)$ растягиваются или сжимаются с коэффициентом $b$ араллельно оси х. Период меняется. Общая формула такова:
$y=\sin(b\cdot x)$
$y=\cos(b\cdot x)$
$y=\cos(b\cdot x)$
!
Запомните
- Если $|b|$ > 1, график сжат (период меняется. Общая формула такова).
- Если $|b|$ < 1, график растянут (период увеличивается).
- Если $b$ < 0, график зеркальный на оси y
- Период (повторения) является $\frac{2\pi}{|b|}$
Например
$\color{green}{g(x)=\sin(\frac12x)}$
$\color{blue}{f(x)=\sin(x)}$
$\color{brown}{h(x)=\sin(2x)}$

