Объяснение на единичной окружности
Круг с радиусом $r=1$ начерченный вокруг начала координат системы, называется единичной окружностью.
Теперь вы можете применить синис и косинус по отношению к единичной окружности:
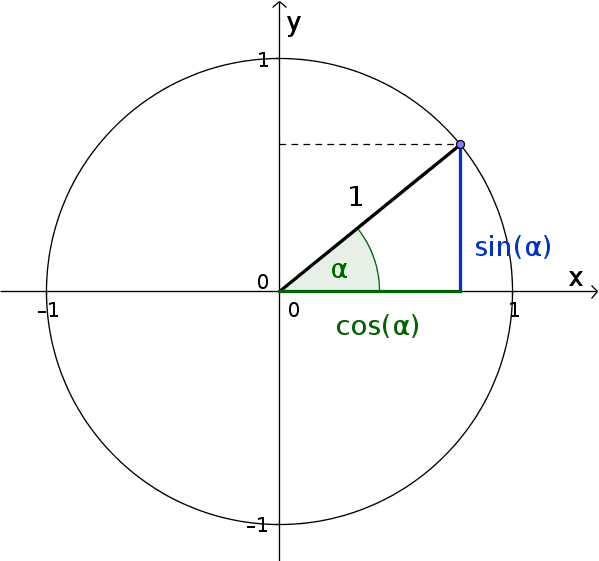
Согласно гипотенузы ($\text{HY}$), единичная окружность равна радиусу $1$, применяется следующие:
$\sin(\alpha)=\frac{\color{blue}{\text{O}}}{\text{HY}}=\frac{\color{blue}{\text{O}}}{1}$ $=\color{blue}{\text{противоположный}}$
$\cos(\alpha)=\frac{\color{green}{\text{A}}}{\text{HY}}=\frac{\color{green}{\text{A}}}{1}$ $=\color{green}{\text{смежный}}$
$\cos(\alpha)=\frac{\color{green}{\text{A}}}{\text{HY}}=\frac{\color{green}{\text{A}}}{1}$ $=\color{green}{\text{смежный}}$
Теперь вы можете представить себе, что гипотенуза вращается против часовой стрелки. Длина смежного или противоположного катета зависит от размера угла $\alpha$.
Чтобы выразить это как функцию, замените $\alpha$ с $x$ и желаемый размер ($\text{противоположный}$/$\text{смежный}$) с $y$:
$y=\sin(x)$
$y=\cos(x)$
$y=\cos(x)$

