Strecken und Stauchen

a) parallel zur y-Achse:

Die Graphen von $y=\sin(x)$ und $y=\cos(x)$ werden mit dem Faktor $a$ parallel zur y-Achse gestreckt bzw. gestaucht. Dabei ändert sich die Amplitude. Die allgemeine Formel lautet:

$y=a\cdot\sin(x)$
$y=a\cdot\cos(x)$

Merke

Wenn $|a|$ > 1, wird der Graph gestreckt.
Wenn $|a|$ < 1, wird der Graph gestaucht.

Wenn $a$ < 0, wird der Graph an der x-Achse gespiegelt
Die Amplitude (maximale Auslenkung) ist $|a|$

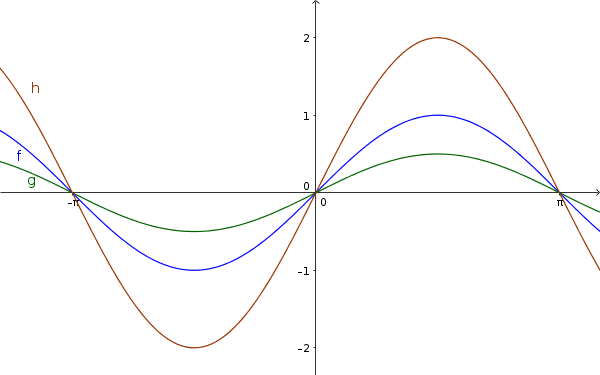
Beispiel

$\color{green}{g(x)=\frac12\sin(x)}$
$\color{blue}{f(x)=\sin(x)}$
$\color{brown}{h(x)=2\sin(x)}$

b) parallel zur x-Achse:

Die Graphen von $y=\sin(x)$ und $y=\cos(x)$ werden mit dem Faktor $b$ parallel zur x-Achse gestreckt bzw. gestaucht. Dabei ändert sich die Periode. Die allgemeine Formel lautet:

$y=\sin(b\cdot x)$
$y=\cos(b\cdot x)$

Merke

Wenn $|b|$ > 1, wird der Graph gestaucht (die Periode wird verkleinert).
Wenn $|b|$ < 1, wird der Graph gestreckt (die Periode wird vergrößert).

Wenn $b$ < 0, wird der Graph an der y-Achse gespiegelt
Die Periode (Wiederholung) ist $\frac{2\pi}{|b|}$

Beispiel

$\color{green}{g(x)=\sin(\frac12x)}$
$\color{blue}{f(x)=\sin(x)}$
$\color{brown}{h(x)=\sin(2x)}$