Math ↠ Trigonometry ↠ Sine, Cosine and Tangent

Sine, Cosine and Tangent

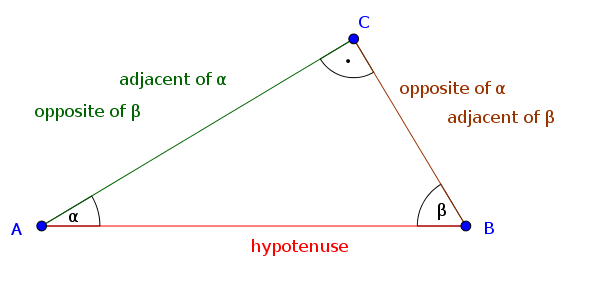
With Sine, Cosine and Tangent in each right-angled triangle, you can calculate the angle of the adjacent/opposite, or the angle itself, if two of the three quantities are known.


!

Remember

  • Sine: $\sin=\frac{\text{opposite}}{\text{hypotenuse}}$
  • Cosine: $\cos=\frac{\text{adjacent}}{\text{hypotenuse}}$
  • Tangent: $\tan=\frac{\text{opposite}}{\text{adjacent}}$

If you use the pages now, we find in our triangle ABC with $\gamma=90^\circ$:

  • $\sin(\alpha)=\frac{a}{c}$ and $\sin(\beta)=\frac{b}{c}$
  • $\cos(\alpha)=\frac{b}{c}$ and $\cos(\beta)=\frac{a}{c}$
  • $\tan(\alpha)=\frac{a}{b}$ and $\tan(\beta)=\frac{b}{a}$

Example

Given is a right triangle with $\beta=90^\circ$, $\alpha=60^\circ$ and $c=4$. Calculate $b$.


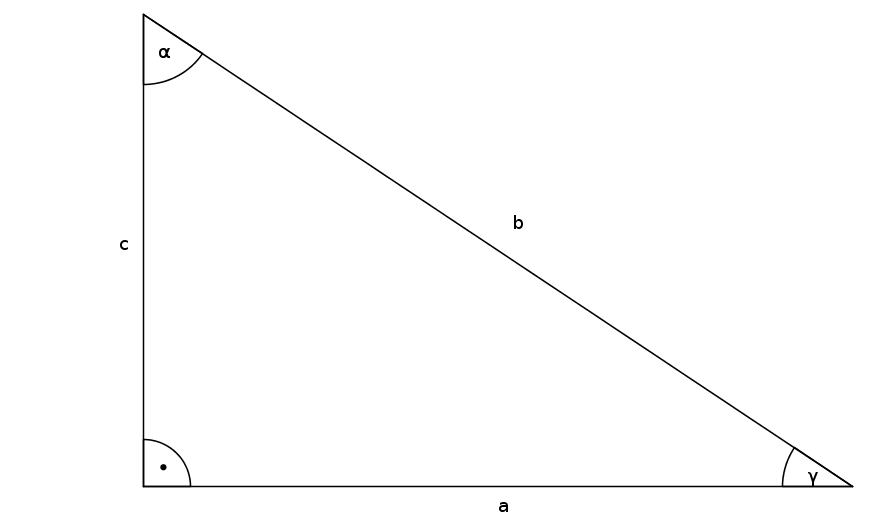
  1. Find the right formula


    $\cos=\frac{\text{adjacent}}{\text{hypotenuse}}$
    $\cos(\alpha)=\frac{c}{b}$

  2. Change the formula


    $\cos(\alpha)=\frac{c}{b}\quad|\cdot b$
    $\cos(\alpha)\cdot b=c\quad|:\cos(\alpha)$
    $b=\frac{c}{\cos(\alpha)}$

  3. Insert and calculate


    $b=\frac{4}{\cos(60^\circ)}=8$