Law of sines

The sine rule is applicable in any triangle, if either

• one side and two angles
or
• two sides and one angle are given.

In the second case, the angle must be opposite to one of the two given sides. Otherwise, you need the cosine rule.

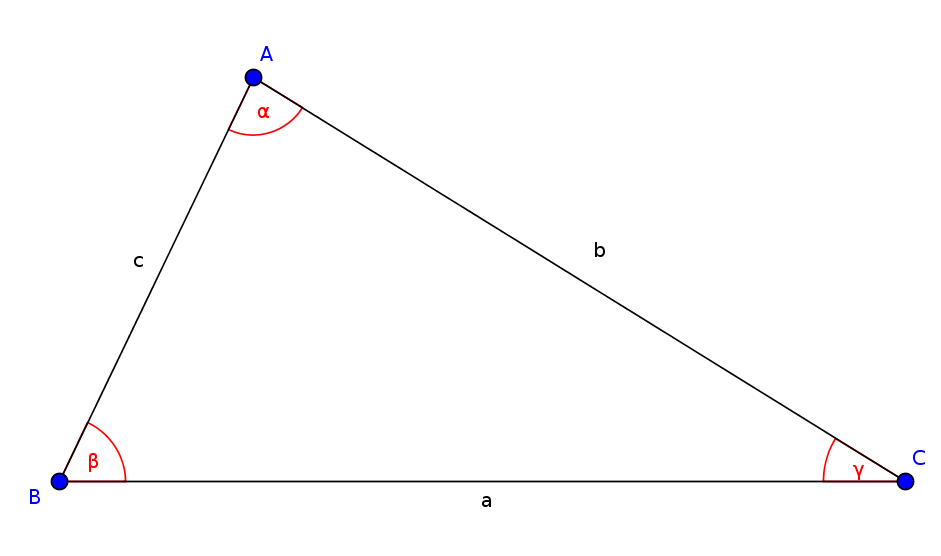
In our triangle ABC, the sine rule says:

• $\frac{a}{b}=\frac{\sin(\alpha)}{\sin(\beta)}$


• $\frac{b}{c}=\frac{\sin(\beta)}{\sin(\gamma)}$


• $\frac{c}{a}=\frac{\sin(\gamma)}{\sin(\alpha)}$


• $\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}$

Example

Given is a triangle with $a=7$, $c=4$ and $\gamma=30^\circ$. Calculate the angle $\alpha$.

1. Find the right formula

   
   $\frac{a}{c}=\frac{\sin(\alpha)}{\sin(\gamma)}$

2. Change the formula

   
   $\frac{a}{c}=\frac{\sin(\alpha)}{\sin(\gamma)}\quad|\cdot\sin(\gamma)$
   $\sin(\alpha)=\frac{a}{c}\cdot\sin(\gamma)$

3. Insert and calculate

   
   $\sin(\alpha)=\frac{7}{4}\cdot\sin(30^\circ)$
   $\alpha=\sin^{-1}(\frac{7}{4}\cdot\sin(30^\circ))\approx61^\circ$