Law of cosines

The cosine rule is applicable in any triangle, if either

• three sides
or
• two sides and the (included) angle are given.

In the second case, the angle cannot be opposite to either of the two given sides. Otherwise, you need the sine rule.

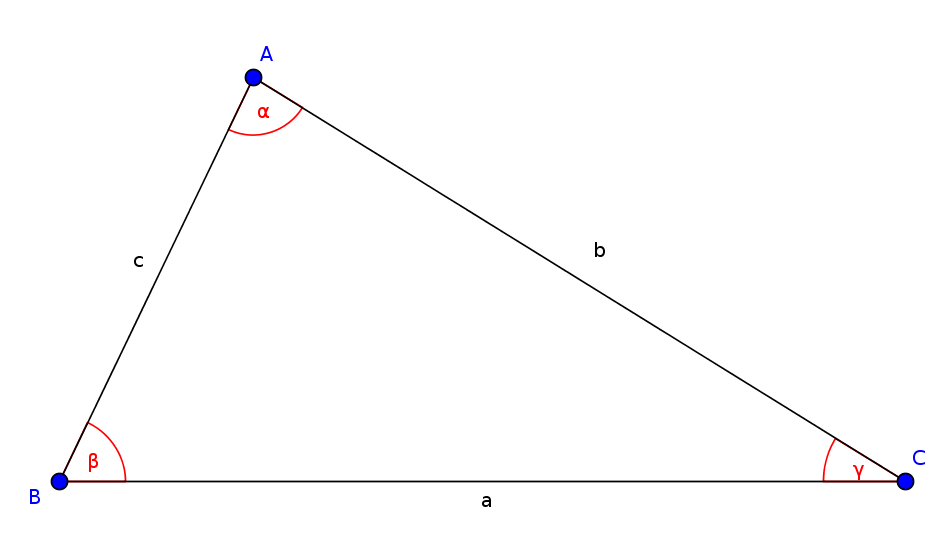
In triangle ABC, the cosine rule says:

• $a^2=b^2+c^2-2bc\cdot\cos(\alpha)$


• $b^2=a^2+c^2-2ac\cdot\cos(\beta)$


• $c^2=a^2+b^2-2ab\cdot\cos(\gamma)$

Example

Given is a triangle with $a=7$, $c=4$ and $\beta=89^\circ$. Calculate the $b$.

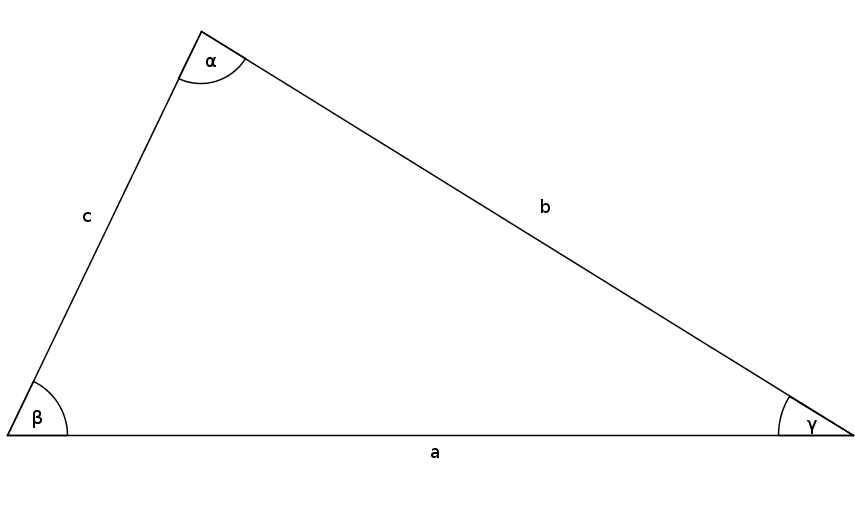
1. Find the right formula

   
   $b^2=a^2+c^2-2ac\cdot\cos(\beta)$

2. Insert and calculate

   
   $b^2=7^2+4^2-2\cdot7\cdot4\cdot\cos(89^\circ)$
   $b^2=65-56\cdot\cos(89^\circ)\quad|\sqrt{}$
   $b=\sqrt{65-56\cdot\cos(89^\circ)}\approx8$