Свойства косинусов

Закон косинусов применим к любому треугольнику, если даны

• три стороны
или
• две стороны и угол .

Во втором случае, угол не может быть противолежащим ни к одной из двух данных сторон. В противном случае применяется закон синусов.

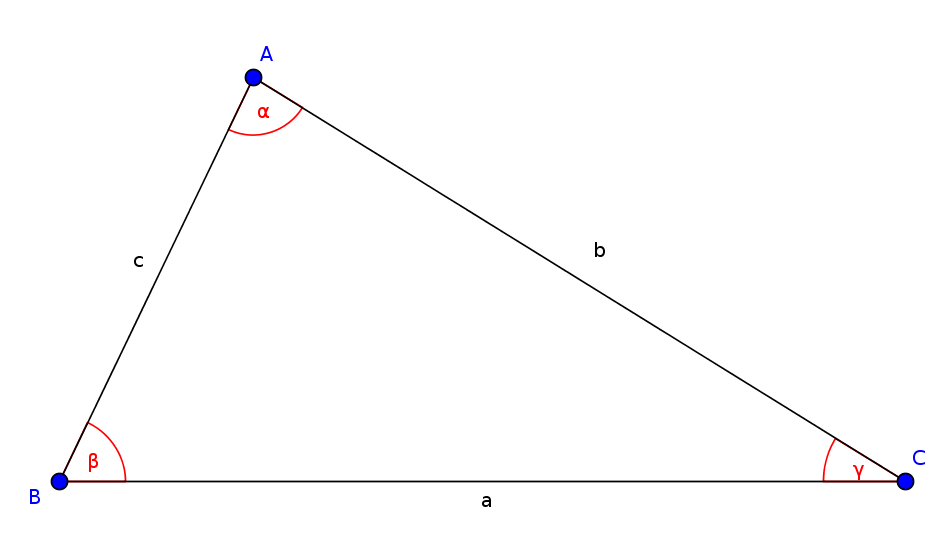
В треугольнике ABC, закон косинусов гласит:

• $a^2=b^2+c^2-2bc\cdot\cos(\alpha)$


• $b^2=a^2+c^2-2ac\cdot\cos(\beta)$


• $c^2=a^2+b^2-2ab\cdot\cos(\gamma)$

Пример

Дан треугольник с $a=7$, $c=4$ и $\beta=89^\circ$. Вычислите $b$.

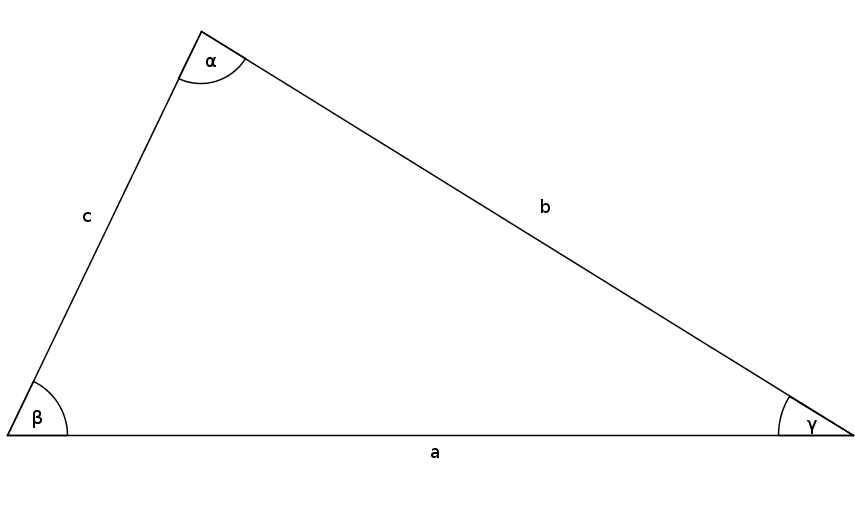
1. Найдите необходимую формулу

   
   $b^2=a^2+c^2-2ac\cdot\cos(\beta)$

2. Подставьте и вычислите

   
   $b^2=7^2+4^2-2\cdot7\cdot4\cdot\cos(89^\circ)$
   $b^2=65-56\cdot\cos(89^\circ)\quad|\sqrt{}$
   $b=\sqrt{65-56\cdot\cos(89^\circ)}\approx8$