Sinus, Kosinus und Tangens

Mit Sinus, Kosinus und Tangens kann man in jedem rechtwinkligen Dreieck die Ankathete/Gegenkathete eines Winkels oder den Winkel selbst berechnen, wenn zwei der drei Größen bekannt sind.

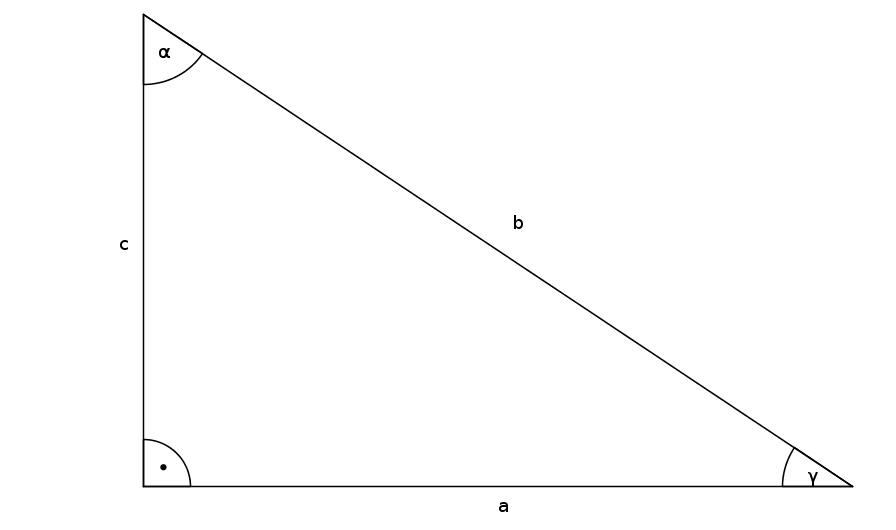
Wenn man jetzt die Seiten einsetzt, ergibt sich in unserem Dreieck ABC mit $\gamma=90^\circ$:

• $\sin(\alpha)=\frac{a}{c}$ und $\sin(\beta)=\frac{b}{c}$
• $\cos(\alpha)=\frac{b}{c}$ und $\cos(\beta)=\frac{a}{c}$
• $\tan(\alpha)=\frac{a}{b}$ und $\tan(\beta)=\frac{b}{a}$

Beispiel

Gegeben ist ein rechtwinkliges Dreieck mit $\beta=90^\circ$, $\alpha=60^\circ$ und $c=4$. Berechne $b$.

1. Passende Formel raussuchen

   
   $\cos=\frac{\text{Ankathete des Winkels}}{\text{Hypotenuse}}$
   $\cos(\alpha)=\frac{c}{b}$

2. Formel umstellen

   
   $\cos(\alpha)=\frac{c}{b}\quad|\cdot b$
   $\cos(\alpha)\cdot b=c\quad|:\cos(\alpha)$
   $b=\frac{c}{\cos(\alpha)}$

3. Einsetzen und ausrechnen

   
   $b=\frac{4}{\cos(60^\circ)}=8$