Verschieben der Normalparabel

a) entlang der y-Achse

Die Normalparabel lässt sich mit dem Parameter $c$ in y-Richtung verschieben. Die allgemeine Formel dazu ist:

$y=x^2+c$

Merke

Wenn $c$ > 0, wird der Graph nach oben verschoben.
Wenn $c$ < 0, wird der Graph nach unten verschoben.

Beispiel

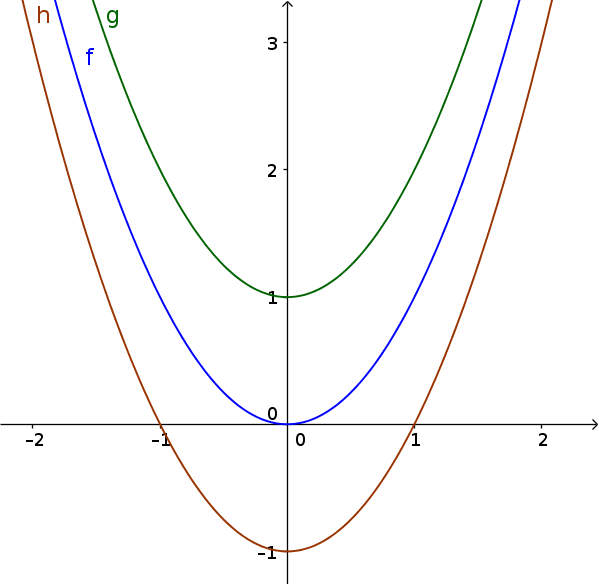
$\color{green}{g(x)=x^2+1}$
$\color{blue}{f(x)=x^2}$
$\color{brown}{h(x)=x^2-1}$

$Verschiebung in y-Richtung$

b) entlang der x-Achse

Die Normalparabel lässt sich mit dem Parameter $d$ in x-Richtung verschieben. Die allgemeine Formel dazu ist:

$y=(x+d)^2$

Merke

Wenn $d$ < 0, wird der Graph nach rechts verschoben.
Wenn $d$ > 0, wird der Graph nach links verschoben.

Beispiel

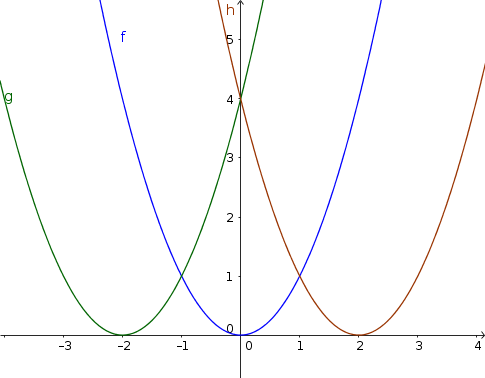
$\color{green}{g(x)=(x+2)^2}$
$\color{blue}{f(x)=x^2}$
$\color{brown}{h(x)=(x-2)^2}$

$Verschiebung in x-Richtung$

Verschiebung Parabel/quadratische Funktion

Kooperation mit dem Kanal von Mister Mathe

Um eine Parabel nach oben oder unten zu verschieben, hängt man dazu einfach den Wert $c$ an die Gleichung: $f(x)=x^2+c$. Die Verschiebung in y-Richtung ist sehr intuitiv, da bei einem positiven Wert der Graph nach oben und bei einem negativen Wert nach unten verschoben wird.

Bei der Verschieben in x-Richtung sollte man aufpassen. Hier wird mit dem Wert $d$ in der Funktionsgleichung $f(x)=(x+d)^2$ verschoben. Dabei gilt, dass ein negativer Wert den Graphen nach rechts ("in positive Richtung") und ein positiver nach links ("in negative Richtung") verschiebt.