Shifting the standard parabola
a) along the y-axis
The standard parabola can be moved with the parameter $c$ in y-direction. The general formula is:
$y=x^2+c$
!
Remember
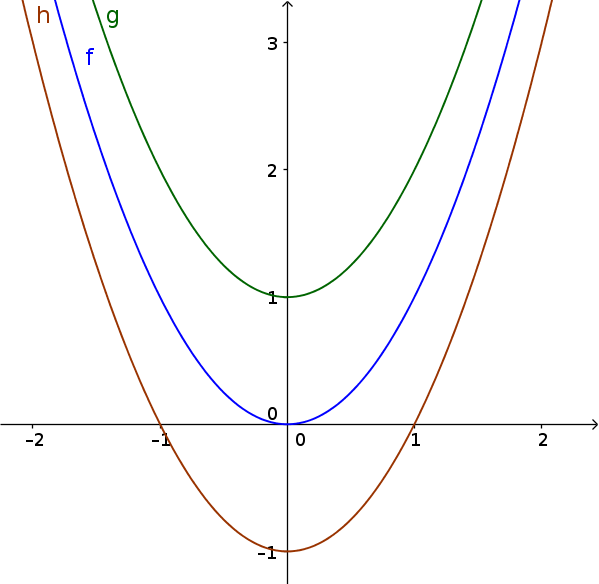
- If $c$ > 0, the graph is shifted up.
- If $c$ < 0, the graph is shifted down.
Example
$\color{green}{g(x)=x^2+1}$
$\color{blue}{f(x)=x^2}$
$\color{brown}{h(x)=x^2-1}$
b) along the x-axis
The standard parabola can be moved with the parameter $d$ in x-direction. The general formula is:
$y=(x+d)^2$
!
Remember
- If $d$ < 0, the graph is shifted to the right.
- If $d$ > 0, the graph is shifted to the left.
Example
$\color{green}{g(x)=(x+2)^2}$
$\color{blue}{f(x)=x^2}$
$\color{brown}{h(x)=(x-2)^2}$

