Mathe ↠ Quadratische Funktionen

Quadratische Funktionen

Eine quadratische Funktion ist jede Funktion mit der allgemeinen Gleichung:

$f(x)=ax^2+bx+c$

Graph einer quadratischen Funktion

Den Graphen einer quadratischen Funktion bezeichnet man als Parabel.

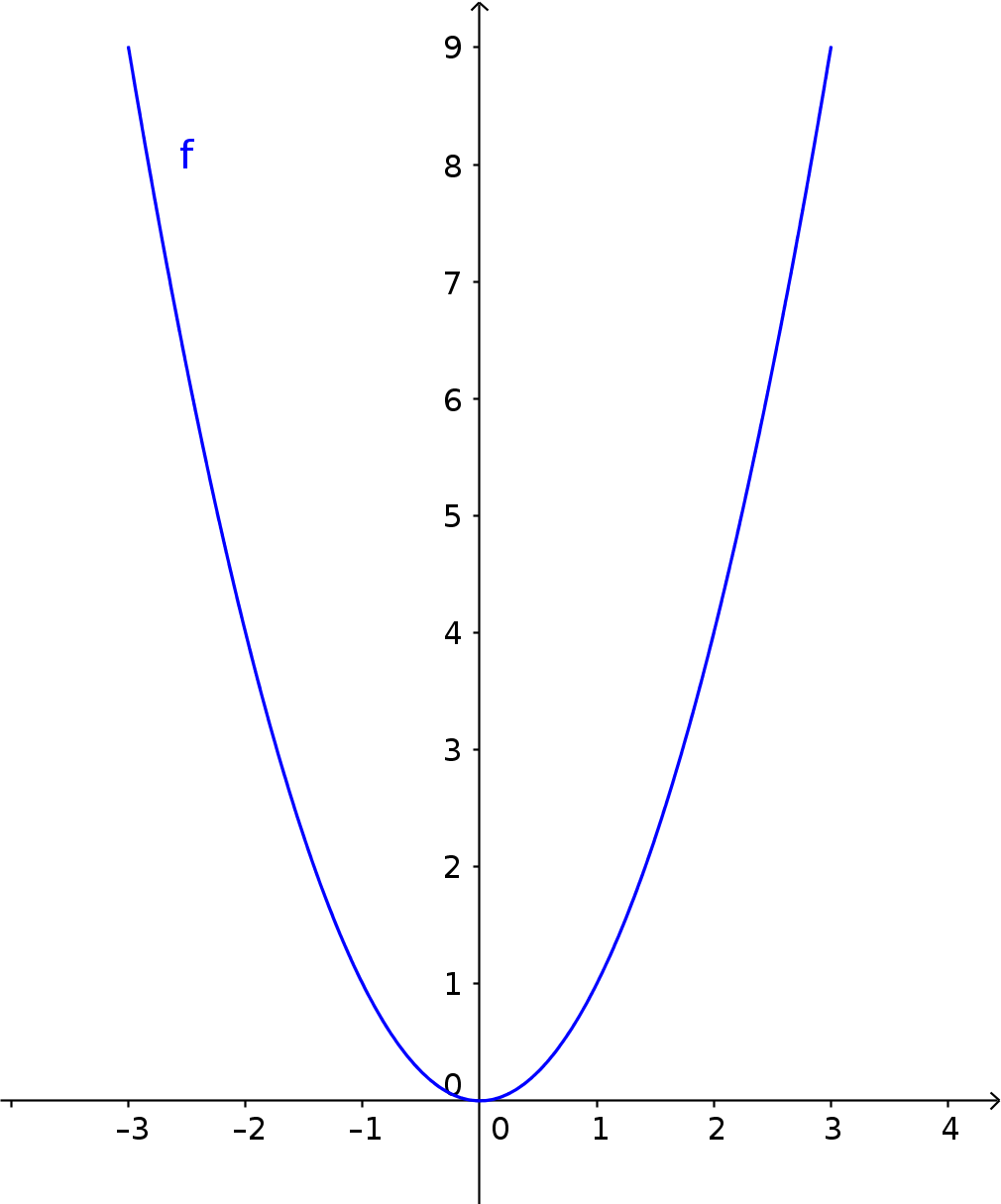
Normalparabel

In der Abbildung handelt es sich um die einfachste quadratische Funktion mit der Funktionsgleichung $f(x)=x^2$. Ihr Graph ist die sogenannte Normalparabel.

Strecken und Stauchen

Die Normalparabel lässt sich mit dem Parameter $a$ strecken und stauchen.

$f(x)=ax^2$
!

Merke

  • Wenn $|a|$ > 1, ist der Graph steiler als die Normalparabel und wird gestreckt.
  • Wenn $|a|$ < 1, ist der Graph flacher als die Normalparabel und wird gestaucht.

Spiegeln der Normalparabel

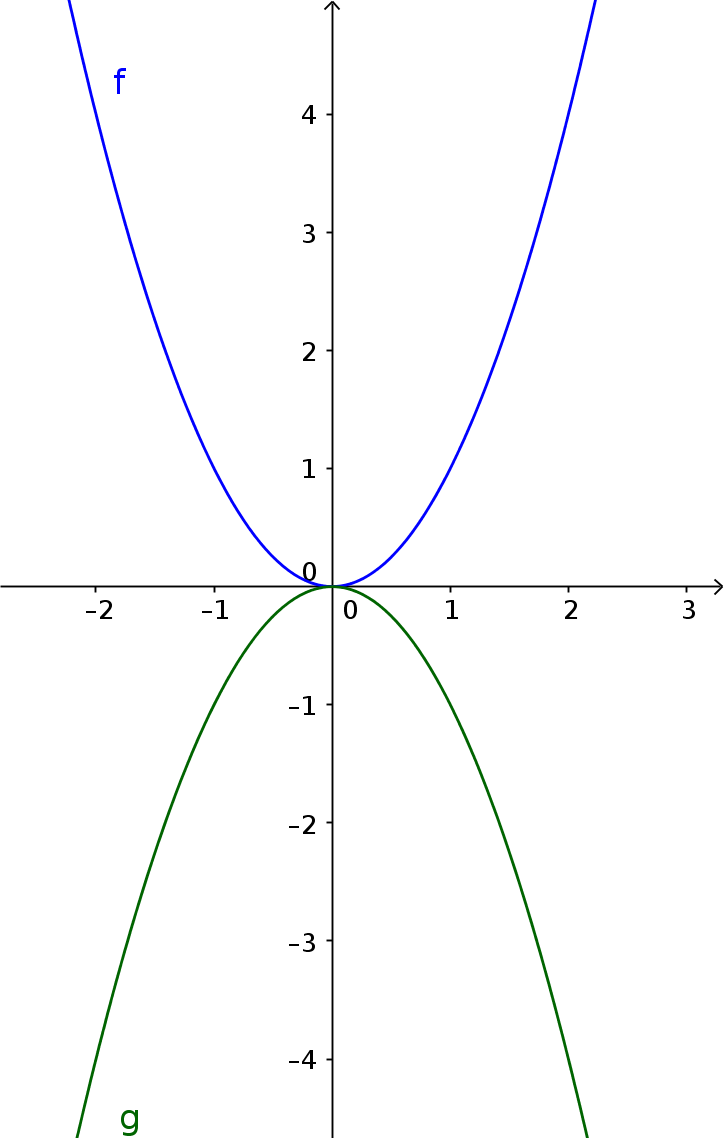
Die Normalparabel lässt sich mit einem negativen Parameter $a$ auch spiegeln.

Beispiel

$\color{blue}{f(x)=x^2}$
$\color{green}{g(x)=-x^2}$

Spiegeln der Normalparabel

Verschieben der Normalparabel

Je nach Funktionsgleichung kann man eine Parabel auch in x- oder y-Richtung verschieben

Entlang der y-Achse

$f(x)=x^2+c$

Mit dem Paramter $c$ kann die Normalparabel in y-Richtung, also nach oben und unten, verschoben werden.

!

Merke

  • Wenn $c$ > 0, wird der Graph nach oben verschoben.
  • Wenn $c$ < 0, wird der Graph nach unten verschoben.

Entlang der x-Achse

$y=(x+d)^2$

Die Normalparabel lässt sich mit dem Parameter $d$ in x-Richtung verschieben.

!

Merke

  • Wenn $d$ < 0, wird der Graph nach rechts verschoben.
  • Wenn $d$ > 0, wird der Graph nach links verschoben.

Scheitelpunktform

Durch die Möglichkeiten des Verschiebens und Streckens erhält man folgende sogenannte Scheitelpunktform, aus der sich der Scheitelpunkt $S(\color{blue}{d}|\color{green}{c})$ der Parabel direkt ablesen lässt. Als Scheitelpunkt bezeichnet man den höchsten (bei nach unten geöffneter Parabel) bzw. tiefsten Punkt (bei nach oben geöffneter Parabel) der Funktion.

$f(x)=a(x-\color{blue}{d})^2+\color{green}{c}$

Um aus der allgemeinen Form $f(x)=ax^2+bx+c$ in die Scheitelpunktform zu kommen, nutzt man die quadratische Ergänzung.

Quiz über Quadratische Funktionen starten