Strecken und Stauchen der Normalparabel

Die Normalparabel lässt sich mit dem Parameter $a$ strecken und stauchen. Die allgemeinen Formel dazu ist:

$y=ax^2$

Merke

Wenn $|a|$ > 1, ist der Graph steiler als die Normalparabel und wird gestreckt.
Wenn $|a|$ < 1, ist der Graph flacher als die Normalparabel und wird gestaucht.

Beispiel

$\color{green}{g(x)=\frac12x^2}$
$\color{blue}{f(x)=x^2}$
$\color{brown}{h(x)=2x^2}$

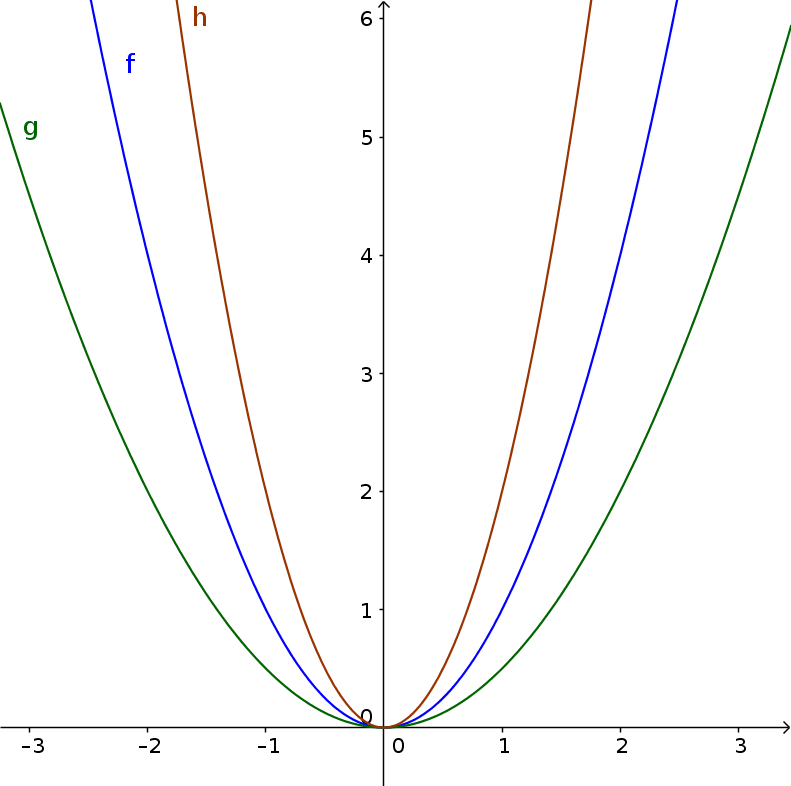
$Strecken und Stauchen$

Streckung/Stauchung Parabel/Quadratische Funktion

Kooperation mit dem Kanal von Mister Mathe

Mit dem Streckfaktor $a$ kann die Parabel der quadratischen Funktion $f(x)=ax^2$ gestreckt oder gestaucht werden. Beim Strecken wird die Parabel dabei schmaler, während sie beim Stauchen breiter wird.

Beachte, dass es dabei auf den Betrag von $a$ ankommt:

Für $a<-1$ und $a>1$ (also $|a| > 1$) ist die Parabel gestreckt
Für $-1 < a < 1$ (also $|a| < 1$) ist die Parabel gestaucht
bei $a=1$ handelt es sich um die Normalparabel

Für negative $a$ wird die Parabel zudem an der x-Achse gespiegelt und ist nach unten geöffnet.