Spiegeln der Normalparabel
Die Normalparabel kann man mit dem Parameter $a$ auch spiegeln. Die allgemeine Formel dazu ist:
$y=ax^2$
!
Merke
- Wenn $a$ > 0, ist die Parabel nach oben geöffnet.
- Wenn $a$ < 0, ist die Parabel nach unten geöffnet.
Beispiel
$\color{blue}{f(x)=x^2}$
$\color{green}{g(x)=-x^2}$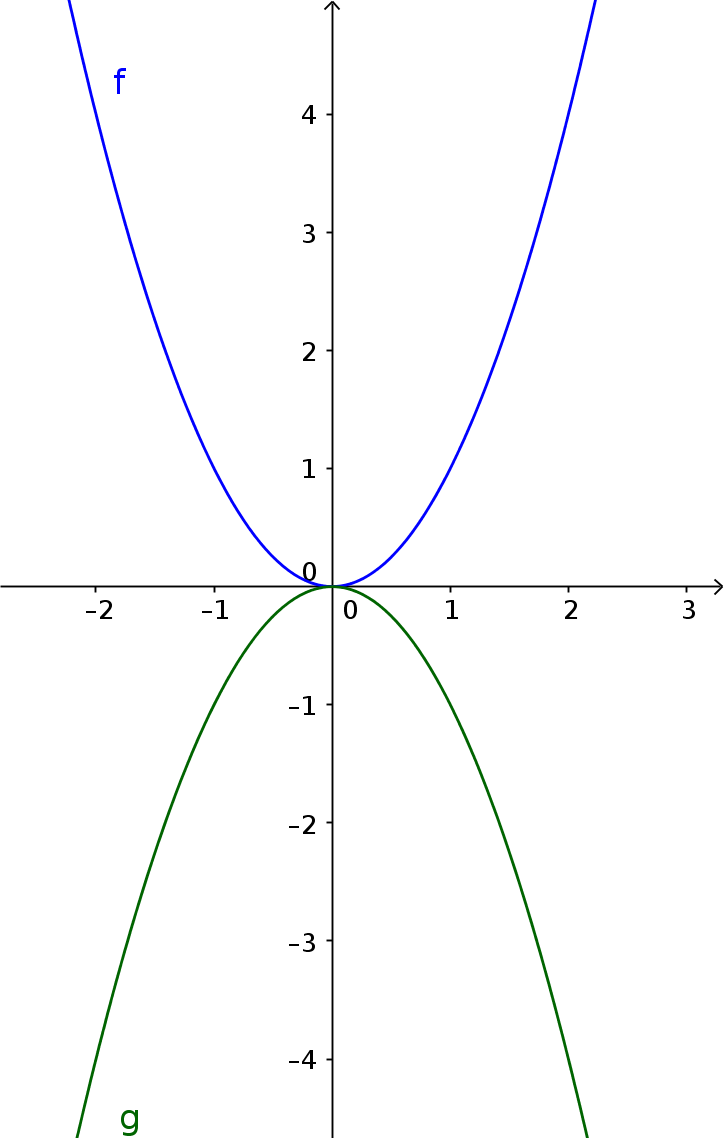
Spiegelung Parabel/quadratische Funktion
Kooperation mit dem Kanal von Mister Mathe
Der Streckfaktor $a$ kann die Parabel der quadratischen Funktion $f(x)=ax^2$ nicht nur strecken und stauchen, sondern auch spiegeln.
Die Spiegelung erfolgt dabei an der waagerechten Geraden, die durch den Scheitelpunkt veläuft. Ein positiver Streckfaktor bedeutet eine nach oben geöffnete und ein negativer eine nach unten geöffnete Parabel.

