Flächeninhalt unter Funktionsgraph
Der Flächeninhalt zwischen einem Graphen und der x-Achse lässt sich mit dem bestimmten Integral berechnen.
Hier ist dazu eine kurze Übersicht. Mehr zur Flächenberechnung mit Integralen findest du im entsprechenden Artikel.
!
Merke
Beim bestimmten Integral gehen die Flächenstücke, welche oberhalb der x-Achse liegen, positiv und, die unterhalb, negativ ein.
Funktionen ohne Vorzeichenwechsel
Der Flächeninhalt unter einer Funktion $f(x)$ ohne Vorzeichenwechsel über $[a; b]$ entspricht dem Betrag des bestimmten Integrals.
$A=|\int_a^b f(x)\,\mathrm{d}x|$
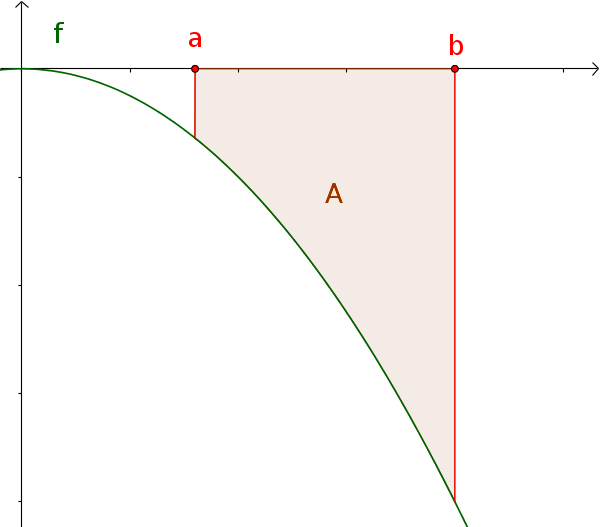
siehe Flächenberechnung
Funktionen mit Vorzeichenwechsel
Die Fläche liegt teilweise über und teilweise unter der x-Achse. Die Flächenstücke müssen also getrennt berechnet und addiert werden.
$A=A_1+A_2$

siehe Flächenberechnung durch Intervallaufteilung
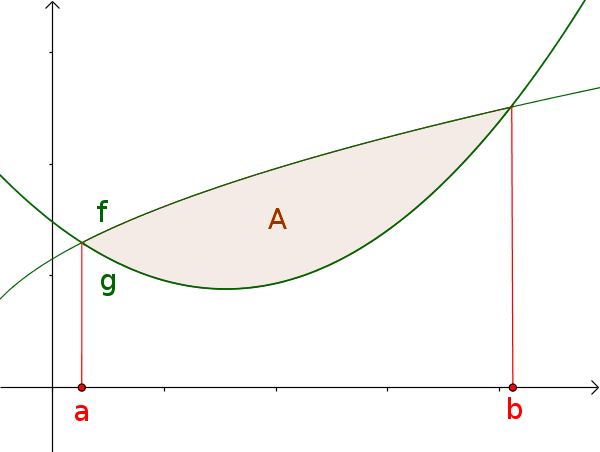
Fläche zwischen Funktionsgraphen
Die eingeschlossene Fläche im Intervall $[a; b]$ berechnet sich mit der Formel:
$A=|\int_a^b (f(x)-g(x))\,\mathrm{d}x|$