Area under a curve
The area between a curve and the x-axis can be calculated with the definite integral.
Here is a short overview. You can find more information about calculating areas with integrals in the corresponding article.
!
Remember
For the definite integral, the partitions above the x-axis are positive and those below, negative.
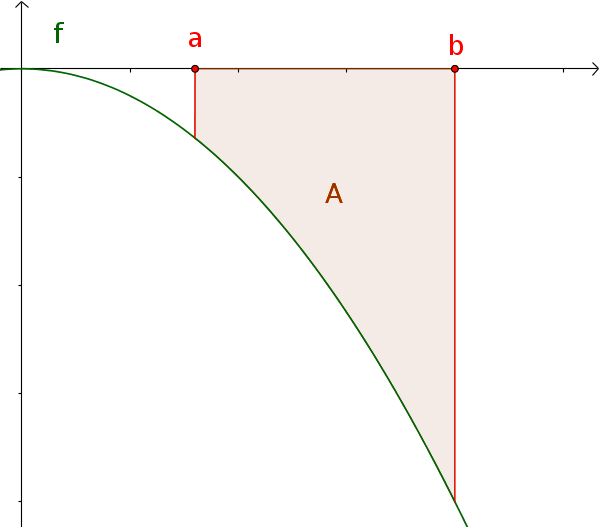
Functions without change of sign
The area under a function $f(x)$ without change of sign over $[a; b]$ corresponds to the absolute value of the definite integral.
$A=|\int_a^b f(x)\,\mathrm{d}x|$
Functions with change of sign
The area is partly above and partly below the x-axis. The divided areas must therefore be calculated and added separately.
$A=A_1+A_2$

see calculating areas by partitioning the interval
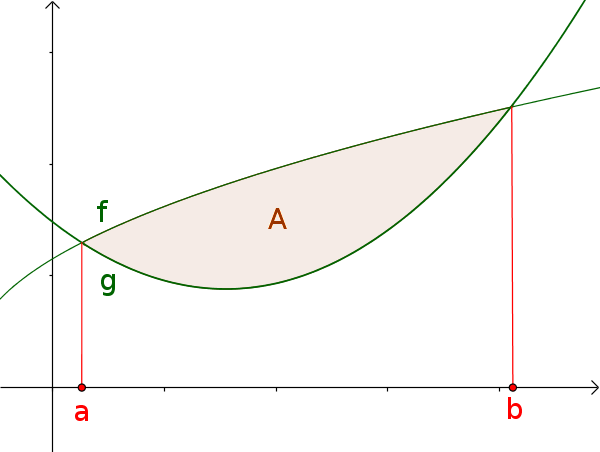
Area between curves
The enclosed area in the interval $[a; b]$ is calculated by the formula:
$A=|\int_a^b (f(x)-g(x))\,\mathrm{d}x|$